16037. Точка O
— центр описанной окружности остроугольного треугольника ABC
, H
— ортоцентр треугольника. Прямая OH
пересекает стороны CA
и CB
в точках K
и L
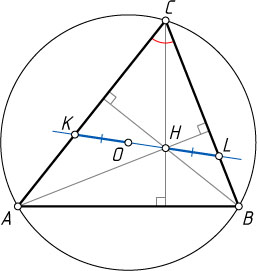
соответственно, причём OK=HL
и точки L
, H
, O
и K
расположены так, как указано на рисунке. Найдите угол ACB
.
Ответ. 60^{\circ}
.
Решение. Пусть углы, противолежащие сторонам BC=a
, AC=b
и AB=c
треугольника, равны \alpha
, \beta
и \gamma
соответственно, а R
— радиус описанной окружности треугольника ABC
. Обозначим \angle CKO=\theta
.
Из точки O
опустим перпендикуляр OP
на AB
. Тогда (см. задачу 1257)
CH=2OP=2OA\cos\angle AOP=2R\cos\gamma.
Поскольку \angle KCO=\angle HCL=90^{\circ}-\beta
(см. задачу 20), получаем
\frac{R}{\sin\theta}=\frac{CO}{\sin\theta}=\frac{KO}{\sin\angle KCO}=\frac{HL}{\sin\angle HCL}=\frac{CH}{\sin\angle CLH}=
=\frac{2OP}{\sin\angle CLH}=\frac{2R\cos\gamma}{\sin\angle CLH},
откуда
\sin\angle CLH=2\sin\theta\cos\gamma=\sin(\theta+\gamma)+\sin(\theta-\gamma).
При этом
\theta+\gamma+\angle CLH=180^{\circ}~\Rightarrow~\sin\angle CLH=\sin(\theta+\gamma).
Значит, \sin(\theta-\gamma)=0
. Следовательно, \theta=\gamma
.
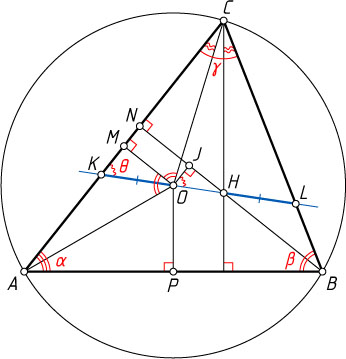
Пусть BN
— высота треугольника ABC
, а M
и J
— проекции точки O
на прямые CA
и NB
соответственно. Тогда OMNJ
— прямоугольник, а M
— середина стороны CA
. Тогда
\tg\gamma=\tg\theta=\tg\angle JOH=\frac{HJ}{OJ}=\frac{HN-JN}{MN}=\frac{HN-OM}{AN-AM}=
=\frac{CH\cos\alpha-OA\cos\angle AOM}{AB\cos\alpha-\frac{1}{2}AC}=\frac{2OP\cos\alpha-OA\cos\beta}{c\cos\alpha-\frac{b}{2}}=
=\frac{2\cos\gamma\cos\alpha+\cos(\alpha+\gamma)}{2\sin\gamma\cos\alpha-\sin\beta}=\frac{2\cos\gamma\cos\alpha+\cos(\alpha+\gamma)}{2\sin\gamma\cos\alpha-\sin(\alpha+\gamma)}=
=\frac{3\cos\gamma\cos\alpha-\sin\alpha\sin\gamma}{\sin\gamma\cos\alpha-\sin\alpha\cos\gamma}=\frac{3-\tg\alpha\tg\gamma}{\tg\gamma-\tg\alpha},
откуда \tg^{2}\gamma=3
. Следовательно, \gamma=60^{\circ}
.
Источник: Журнал «Crux Mathematicorum». — 1989, № 1, задача 1300 (1987, с. 321), с. 23

