16055. Биссектриса угла при вершине A
треугольника ABC
пересекает сторону BC
в точке D
, а биссектрисы внешних углов при вершинах B
и C
пересекают продолжения сторон AC
и AB
в точках E
и F
соответственно. Перпендикуляры к прямым BC
, AC
и AB
, восставленные в точках соответственно D
, E
и F
, пересекаются в одной точке. Докажите, что AB=AC
.
Решение. Пусть указанные в условии перпендикуляры пересекаются в точке Q
. Тогда
BD^{2}+DQ^{2}=BF^{2}+FQ^{2},
CE^{2}+EQ^{2}=CD^{2}+DQ^{2},
AF^{2}+FQ^{2}=AE^{2}+EQ^{2}.
Сложив эти равенства, получим
(BD^{2}-DC^{2})+(CE^{2}-EA^{2})+(AF^{2}-FB^{2})=0.\eqno(1)
Обозначим BC=a
, CA=b
и AB=c
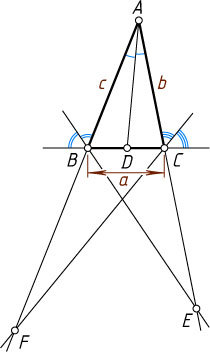
. Рассмотрим случай, изображённый на рисунке (a\lt b
, a\lt c
). По свойству биссектрисы треугольника (см. задачи 1509 и 1645) находим, что
BD=\frac{ac}{b+c},~DC=\frac{ab}{b+c},
CE=\frac{ab}{c-a},~EA=\frac{bc}{c-a},
BF=\frac{ac}{b-a},~AF=\frac{bc}{b-a}.
Подставляя найденные значения в равенство (1), получим
\frac{a^{2}(c^{2}-b^{2})}{(b+c)^{2}}+\frac{b^{2}(a^{2}-c^{2})}{(c-a)^{2}}+\frac{c^{2}(b^{2}-a^{2})}{(b-a)^{2}}=0,
или
\frac{a^{2}(c-b)}{b+c}-\frac{b^{2}(a+c)}{c-a}+\frac{c^{2}(b+a)}{b-a}=0,
\frac{(c-b)(a+b)(a+c)(b+c-a)^{2}}{(b+c)(c-a)(b-a)}=0,
а так как b+c-a\gt0
по неравенству треугольника, то b=c
, или AC=AB
. Что и требовалось доказать.
Аналогично для остальных случаев.
Источник: Австрийские математические олимпиады. — 1991, № 1, задача 1491, с. 30
