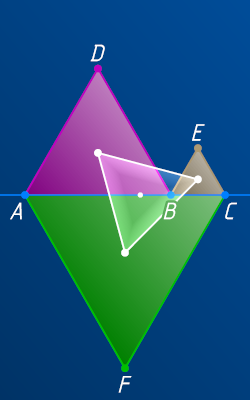
16129. Точки A
, B
и C
лежат на одной прямой, причём точка B
лежит между A
и C
. На отрезках AB
, BC
и AC
построены равносторонние треугольники ABD
, BCE
и CAF
, причём точки D
и E
лежат по одну сторону от прямой AC
, а точка F
— по другую. Докажите, что центры треугольников ABD
, BCE
и CAF
— вершины равностороннего треугольника, а его центр лежит на прямой AC
.
Решение. Введём систему координат xBy
с началом в точке B
, направив ось Bx
по лучу BC
, а ось BY
— по лучу, перпендикулярному AC
и лежащему с точкой D
по одну сторону от прямой AC
. Обозначим AB=a
, BC=b
.
Тогда точки G_{1}\left(-\frac{a}{2};\frac{a\sqrt{3}}{6}\right)
, G_{2}\left(\frac{b}{2};\frac{b\sqrt{3}}{6}\right)
, G_{3}\left(\frac{-a+b}{2};-\frac{(a+b)\sqrt{3}}{6}\right)
— центры равносторонних треугольников ABD
, BCE
и CAF
соответственно. Значит (см. задачу 4200), G\left(\frac{-a+b}{3};0\right)
— точка пересечения медиан треугольника G_{1}G_{2}G_{3}
.
Применив формулу для расстояния между двумя точками (см. задачу 4201), легко проверить, что
G_{1}G_{2}=G_{2}G_{3}=G_{1}G_{3}=\sqrt{\frac{a^{2}+ab+b^{2}}{3}}.
Следовательно, треугольник G_{1}G_{2}G_{3}
равносторонний.
Кроме того, поскольку ордината точки G
равна 0, эта точка лежит на прямой AC
.
Что и требовалось доказать.
Источник: Ирландские математические олимпиады. — 1994
Источник: Журнал «Crux Mathematicorum». — 1998, № 8, задача 2, с. 456
