16191. Вписанная окружность треугольника ABC
касается окружности с диаметром BC
. Докажите, что радиус вневписанной окружности треугольника ABC
, противоположной вершине A
, равен стороне BC
.
Решение. Обозначим BC=a
, CA=b
, AB=c
, p
— полупериметр треугольника ABC
, S
— площадь, r
и r_{a}
— радиусы соответственно вписанной окружности треугольника и вневписанной окружности, противоположной вершине A
.
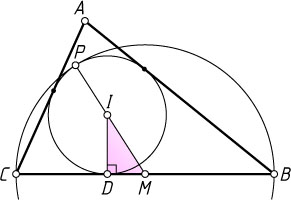
Пусть окружность с центром I
, вписанная в треугольник ABC
, касается стороны BC
в точке D
, вписанная окружность касается окружности с диаметром BC
в точке P
, а M
— середина стороны BC
.
Из прямоугольного треугольника IDM
с гипотенузой
IM=MP-IP=\frac{a}{2}-r
и катетами
ID=r~\mbox{и}~DM=|CM-CD|=\left|\frac{a}{2}-(p-c)\right|
получаем
\left(\frac{a}{2}-r\right)^{2}=r^{2}+\left(\frac{a}{2}-(p-c)\right)^{2}~\Leftrightarrow~\frac{a^{2}}{4}-ar=\left(\frac{a}{2}-\frac{a+b-c}{2}\right)^{2}~\Leftrightarrow
\Leftrightarrow~ar=\frac{a^{2}}{4}-\left(\frac{c-b}{2}\right)^{2}~\Leftrightarrow~ar=\frac{a+c-b}{2}\cdot\frac{a+b-c}{2}=(p-b)(p-c).
В то же время (см. задачи 452, 392 и 2730)
pr=(p-a)r_{a}=\sqrt{p(p-a)(p-b)(p-c)},
поэтому
S^{2}=p(p-a)(p-b)(p-c)=p(p-a)\cdot ar~\Rightarrow
\Rightarrow~ar=\frac{S^{2}}{p(p-a)}=\frac{pr\cdot(p-a)r_{a}}{p(p-a)}=rr_{a}~\Rightarrow~r_{a}=a.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 2002, № 6, задача 2663 (2001, 337), с. 408
