16293. Дан отрезок AB
. Найдите геометрическое место точек пересечения медиан остроугольных треугольников ABC
, если известно, что вершины A
и B
, ортоцентр H
и центр I
вписанной окружности треугольника ABC
лежат на одной окружности.
Ответ. См. рис.
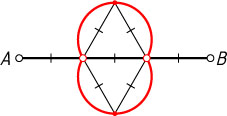
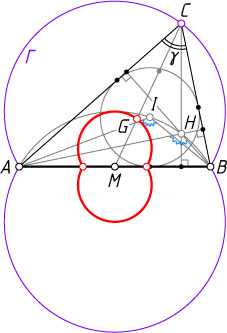
Решение. Обозначим \angle ACB=\gamma
. Тогда (см. задачу 4770)
\angle AIB=90^{\circ}+\frac{\gamma}{2},
а так как
\angle AIB=\angle AHB=180^{\circ}-\gamma,
то
90^{\circ}+\frac{\gamma}{2}=180^{\circ}-\gamma~\Rightarrow~\gamma=60^{\circ}.
Геометрическое место точек C
(обозначим его \Gamma
), из которых отрезок AB
виден под углом 60^{\circ}
— две дуги равных окружностей, симметричные относительно прямой AB
и вмещающие угол 60^{\circ}
(см. задачу 12).
Пусть M
— середина стороны AB
, G
— точка пересечения медиан треугольника ABC
. Тогда MG=\frac{1}{3}MC
(см. задачу 1207). Следовательно, искомое геометрическое место точек G
— образ \Gamma
при гомотетии с центром M
и коэффициентом \frac{1}{3}
.
Источник: Математические олимпиады Чехии и Словакии. — 2006
Источник: Журнал «Crux Mathematicorum». — 2010, № 4, задача 4 (2009, с. 81-82), с. 221

