1207. Теорема о медианах. Докажите, что медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1
, считая от вершины треугольника.
Указание. Докажите, что любые две медианы делятся точкой их пересечения в отношении 2:1
, считая от вершины.
Решение. Первый способ. Докажем сначала, что любые две медианы делятся точкой пересечения в отношении 2:1
.
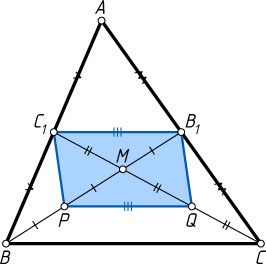
Пусть B_{1}
и C_{1}
— середины сторон AC
и AB
треугольника ABC
, M
— точка пересечения медиан BB_{1}
и CC_{1}
, P
и Q
— середины BM
и CM
. Тогда C_{1}B_{1}
и PQ
— средние линии треугольников ABC
и MBC
. Поэтому C_{1}B_{1}=PQ
и C_{1}B_{1}\parallel PQ
. Значит, четырёхугольник PC_{1}B_{1}Q
— параллелограмм. Его диагонали PB_{1}
и QC_{1}
делятся точкой пересечения M
пополам. Поэтому
BP=PM=MB_{1},~CQ=QM=MC_{1}.
Таким образом, BM:MB_{1}=CM:MC_{1}=2:1
. Аналогично для любой другой пары медиан.
Медиана, проведённая из вершины A
, должна пройти через точку пересечения двух других медиан, так как в противном случае она не разделит каждую из этих медиан в отношении 2:1
.
Второй способ. Пусть A_{1}
, B_{1}
и C_{1}
— середины сторон соответственно BC
, AC
и AB
треугольника ABC
. Тогда
\frac{AB_{1}}{B_{1}C}\cdot\frac{CA_{1}}{A_{1}B}\cdot\frac{BC_{1}}{C_{1}A}=1.
Следовательно, по теореме Чевы (см. задачу 1621) медианы AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке.
Пусть M
— точка пересечения медиан треугольника ABC
. Применяя теорему Менелая (см. задачу 1622) к треугольнику BCC_{1}
и прямой AA_{1}
, получим, что
\frac{CM}{MC_{1}}\cdot\frac{C_{1}A}{AB}\cdot\frac{BA_{1}}{A_{1}B}=1,~\frac{CM}{MC_{1}}\cdot\frac{1}{2}\cdot\frac{1}{1}=1,
откуда \frac{CM}{MC_{1}}=2
. Аналогично \frac{AM}{MA_{1}}=\frac{BM}{MB_{1}}=2
.
Третий способ. Поместим в вершины треугольника ABC
одинаковые массы m
. Тогда центр масс точек A
и B
— середина C_{1}
стороны AB
. Поместим в точку C_{1}
массу 2m
. Тогда центр масс M
точек A
, B
и C
совпадает с центром масс точек C
и C_{1}
(см. задачу 6797). Точка M
лежит на медиане CC_{1}
и делит её в отношении CM:MC_{1}=2:1
(см. задачу 6798). Из единственности центра масс (см. задачу 6796) следует, что точка M
лежит на двух других медианах и делит их в отношении 2:1
, считая от вершины.
Примечание. См. также статью В.Н.Дубровского: «Шесть доказательств теоремы о медианах», Квант, 1990, N1, с.54.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 64
Источник: Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — № 1.41, с. 25-26
Источник: Зетель С. И. Новая геометрия треугольника. — М.: Учпедгиз, 1962. — с. 11
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 1
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3, с. 11; № 14.4, с. 326
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 1, с. 5
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — с. 265
