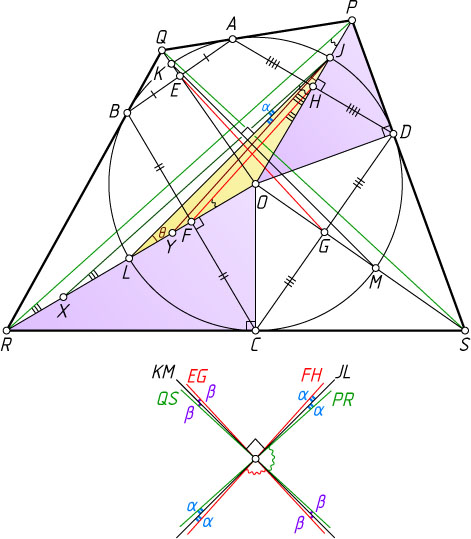
16480. Окружность, вписанная в четырёхугольник PQRS
, касается сторон PQ
, QR
, RS
и SP
в точках A
, B
, C
и D
соответственно. Точки E
, F
, G
и H
— середины отрезков AB
, BC
, CD
и DA
соответственно. Докажите, что угол между диагоналями PR
и QS
равен углу между отрезками EG
и FH
(бимедианами четырёхугольника ABCD
).
Решение. Рассмотрим случай, изображённый на рисунке. Пусть O
— центр окружности, r
— радиус. Точки P
, H
и O
лежат на биссектрисе угла QPS
. На этой же биссектрисе лежат середина J
не содержащей точки B
дуги AD
окружности. Аналогично, середины K
, L
и M
соответствующих дуг AB
, BC
и CD
лежат на биссектрисах углов RQP
, SRQ
и RSP
соответственно. Заметим, что JL\perp MK
(см задачу 28).
Заметим также, что прямые PR
и HF
антипараллельны относительно сторон угла JOL
(т. е. \angle OHF=\angle ORP
и OFH=\angle OPR
), так как DH
и CF
— высоты прямоугольных треугольников ODP
и OCR
, проведённые из вершины прямых углов, и поэтому (см. задачу 2728)
OH\cdot OP=OD^{2}=r^{2}=OC^{2}=OF\cdot OR~\Rightarrow~\frac{OH}{OF}=\frac{OR}{OP}.
Значит, треугольники FOH
и POR
с общим углом при вершине O
подобны, и их соответственные углы равны.
Отметим на луче OR
точки X
и Y
, для которых JX\parallel PR
и JY\parallel HF
. Обозначим через \theta
угол при основании равнобедренного треугольника JOL
. Тогда
\angle XJL=\theta-\angle OXJ=\theta-\angle ORP=\theta-\angle OHF=
=\theta-\angle OJY=\angle LJY.
Значит, прямые HF
и PR
образуют равные углы с прямой JL
(обозначим их \alpha
). Аналогично, прямые QS
и FG
образуют равные углы с прямой KM
(обозначим их \beta
).
Параллельно перенеся все шесть прямых в одну точку, получим, что оба угла между прямыми, параллельными PR
и QS
, и прямыми, параллельными EG
и FH
, равны 90^{\circ}-\alpha-\beta
. Отсюда следует утверждение задачи.
Источник: Журнал «Mathematics Magazine». — 1990, том 63, № 4, задача 1327, с. 275
