16484. Разделим каждую сторону выпуклого четырёхугольника ABCD
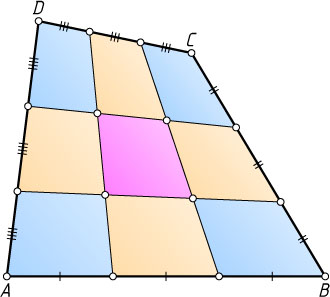
на три равные части и соединим отрезками соответствующие точки на противоположных сторонах (см.рис.).
а) Докажите, что площадь «среднего» четырёхугольника в 9 раз меньше площади четырёхугольника ABCD
.
б) Найдите необходимое и достаточное условия равновеликости всех девяти полученных четырёхугольников.
Ответ. б) Данный четырёхугольник — параллелограмм.
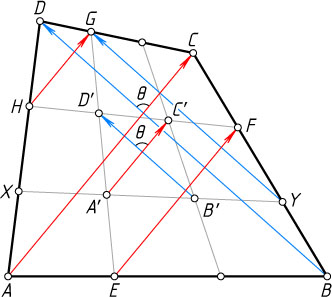
Решение. Введём обозначения, как показано на рисунке. Тогда
\overrightarrow{EF}=\frac{2}{3}\overrightarrow{AC}~\mbox{и}~\overrightarrow{HG}=\frac{1}{3}\overrightarrow{AC}.
Треугольники D'GH
и D'EF
подобны с коэффициентом \frac{GH}{EF}=\frac{1}{2}
, поэтому D'H=\frac{1}{3}HF
. Аналогично, C'F=\frac{1}{3}HF
. Значит, точки D'
и C'
делят отрезок HF
на три равные части. Аналогично для пар точек A'
и B'
, B'
и C'
, A'
и D'
. Тогда
\overrightarrow{A'C'}=\frac{1}{2}\overrightarrow{EF}=\frac{1}{2}\cdot\frac{2}{3}\overrightarrow{AC}=\frac{1}{3}\overrightarrow{AC},
\overrightarrow{B'D'}=\frac{1}{2}\overrightarrow{YG}=\frac{1}{2}\cdot\frac{2}{3}\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BD}.
а) Пусть угол между диагоналями четырёхугольника ABCD
равен \theta
. Тогда угол между диагоналями четырёхугольника A'B'C'D'
тоже равен \theta
. Следовательно (см. задачу 3018),
S_{A'B'C'D'}=\frac{1}{2}A'C'\cdot B'D'\sin\theta=\frac{1}{2}\cdot\frac{1}{3}AC\cdot\frac{1}{3}BD\sin\theta=\frac{1}{9}\cdot\frac{1}{2}AC\cdot BD\sin\theta=\frac{1}{9}S_{ABCD}.
Что и требовалось доказать.
(См. также решение задачи 3207.)
б) Докажем, что все девять четырёхугольников разбиения равновелики тогда и только тогда, когда ABCD
— параллелограмм.
Пусть, например, четырёхугольники AEA'X
и XA'D'H
равновелики. Тогда, поскольку равновелики треугольники EA'X
и D'A'X
, то равновелики и треугольники AEX
и D'HX
с равными основаниями AX
и XH
. Значит, AD\parallel EG
. Остальное аналогично. Необходимость доказана.
Достаточность очевидна.
Источник: Журнал «Mathematics Magazine». — 1991, том 64, № 4, задача 1354, с. 277

