2324. Треугольник ABC
вписан в окружность. Через точку A
проведены хорды, пересекающие сторону BC
в точках K
и L
и дугу BC
в точках M
и N
. Докажите, что если вокруг четырёхугольника KLNM
можно описать окружность, то треугольник ABC
— равнобедренный.
Решение. Угол AKL
равен полусумме дуг AC
и BM
, а угол LNM
— полусумме дуг AB
и BM
(см. задачу 26). Четырёхугольник KLNM
вписанный, поэтому
\angle AKL=180^{\circ}-\angle LKM=\angle LNM,
значит, дуги AB
и AC
равны. Следовательно, стягивающие их хорды AB
и CD
также равны (см. задачу 805), т. е. треугольник ABC
— равнобедренный.
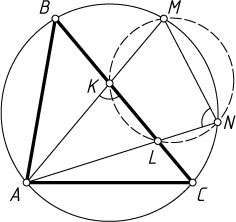
Источник: Турнир городов. — 2000-2001, XXII, осенний тур, старшие классы, тренировочный вариант
