2457. Даны прямая и на ней точки A
и B
. Найдите геометрическое место точек касания окружностей, одна из которых касается данной прямой в точке A
, другая — в точке B
.
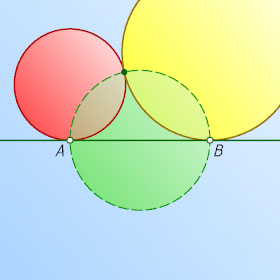
Ответ. Окружность без двух точек.
Указание. Если M
— точка касания указанных окружностей, то \angle AMB=90^{\circ}
.
Решение. Если M
— точка касания окружностей, касающихся данной прямой в точках A
и B
, то \angle AMB=90^{\circ}
(см. задачу 1762). Следовательно, точка M
лежит на окружности с диаметром AB
.
Рассмотрим теперь любую точку P
этой окружности, отличную от A
и B
. Соединим её с центром O
окружности. Впишем в углы AOP
и BOP
окружности, проходящие через точку P
. Эти окружности имеют общую точку P
и общую касательную в этой точке. Следовательно, они касаются в точке P
(см. задачу 1759). Кроме того, поскольку OA=OP
и OB=OP
, одна из них касается прямой AB
в точке A
, а вторая — в точке B
.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — № 112, с. 105
Источник: Пособие по математике для поступающих в вузы / Под ред. Г. Н. Яковлева. — 3-е изд. — М.: Наука, 1988. — № 9, с. 431
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 7.13, с. 184
