2729. Теорема Пифагора. Докажите, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
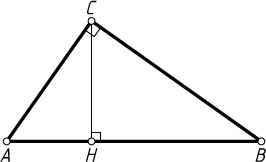
Решение. Первый способ. Пусть CH
— высота прямоугольного треугольника, проведённая из вершины C
прямого угла (рис. 1). Тогда
AC^{2}=AH\cdot AB,~BC^{2}=BH\cdot AB,
(см. задачу 2728). Следовательно,
AC^{2}+BC^{2}=AH\cdot AB+BH\cdot AB=(AH+BH)AB=AB\cdot AB=AB^{2},
что и требовалось доказать.
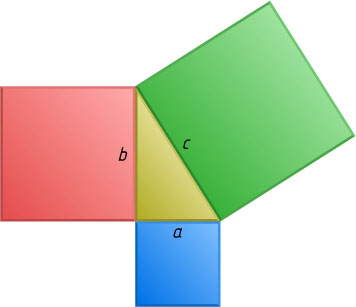
Второй способ. Пусть катеты прямоугольного треугольника равны a
и b
, а гипотенуза равна c
. Построим на катетах и гипотенузе как на сторонах три квадрата (рис. 2). Их площади равны соответственно a^{2}
, b^{2}
и c^{2}
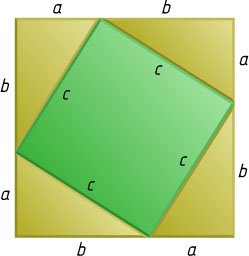
. Докажем, что сумма площадей двух меньших квадратов равна площади большего. Для этого рассмотрим два квадрата со стороной, равной a+b
. Один из них разбивается на четыре прямоугольных треугольника (с катетами a
, b
и гипотенузой c
) и квадрат со стороной c
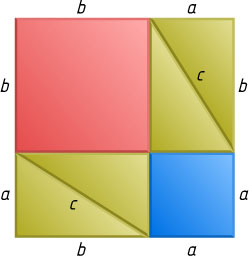
(рис. 3), а второй — на четыре таких же прямоугольных треугольника и два квадрата со сторонами a
и b
(рис. 4). Значит, сумма площадей двух последних квадратов равна площади квадрата со стороной c
. Следовательно,
a^{2}+b^{2}=c^{2}.
Третий способ. Пусть катеты и гипотенуза прямоугольного треугольника равны соответственно a
, b
и c
, площадь равна S
, а радиус вписанной окружности равен r
. Тогда (см. задачу 217)
r=\frac{1}{2}(a+b-c),~S=\frac{1}{2}(a+b+c)r,~S=\frac{1}{2}ab,
поэтому
(a+b+c)(a+b-c)=2ab,~(a+b)^{2}-c^{2}=2ab,
откуда получаем, что
a^{2}+b^{2}=c^{2}.
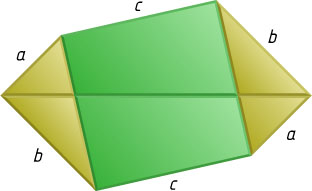
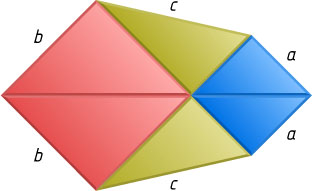
Четвёртый способ. На противоположных сторонах квадрата со стороной c
построим прямоугольные треугольники с катетами a
, b
и гипотенузой c
(рис. 5). Получим шестиугольник, площадь которого равна сумме площадей квадрата и двух прямоугольных треугольников.
Второй шестиугольник построим так: на продолжениях двух соседних сторон квадрата со стороной b
за их общую вершину построим квадрат со стороной a
и соединим две его вершины с двумя вершинами первого квадрата (рис. 6). Площадь этого шестиугольника равна сумме площадей квадратов со сторонами a
и b
и двух прямоугольных треугольников с катетами a
и b
.
В обоих шестиугольниках проведём большие диагонали. Каждая из них разбивает свой шестиугольник на два равновеликих (даже равных) четырёхугольника. Все четыре полученных четырёхугольника равновелики (даже равны). Значит, равновелики и шестиугольники. Поэтому сумма площадей квадратов со сторонами a
и b
равна площади квадрата со стороной c
. Следовательно,
a^{2}+b^{2}=c^{2}.
(Это доказательство приписывается Леонардо да Винчи.)
Примечание. См. также статью Р.Сарбаша «Теорема Пифагора», Квант, 2004, N6, с.32-33.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 122, 234-235
Источник: Шень А. Х. Геометрия в задачах. — М.: МЦНМО, 2013. — № 579, с. 168, № 590, с. 175





