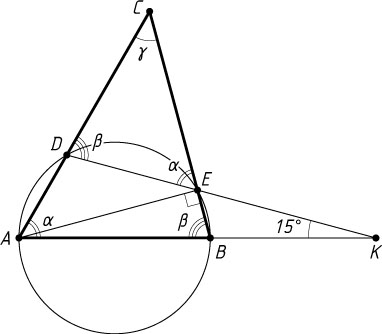
2756. На стороне AB
треугольника ABC
как на диаметре построена окружность, пересекающая стороны AC
и BC
в точках D
и E
соответственно. Прямая DE
делит площадь треугольника ABC
пополам и образует с прямой AB
угол 15^{\circ}
. Найдите углы треугольника ABC
.
Ответ. 60^{\circ}
, 75^{\circ}
, 45^{\circ}
.
Указание. Треугольник CDE
подобен треугольнику CBA
с коэффициентом |\cos\angle ACE|
.
Решение. Обозначим углы при вершинах A
, B
и C
треугольника ABC
через \alpha
, \beta
и \gamma
соответственно. Поскольку точка C
лежит вне окружности с диаметром AB
, то угол при вершине C
— острый (см. задачу 1772), т. е. \gamma\lt90^{\circ}
.
Точки A
, D
, E
и B
лежат на одной окружности, поэтому
\angle CDE=180^{\circ}-\angle ADE=\angle ABC=\beta.
Аналогично докажем, что \angle CED=\alpha
.
Треугольник CDE
подобен треугольнику CBA
(см. задачу 19), причём коэффициент подобия равен квадратному корню из отношения площадей этих треугольников, т. е. k=\frac{1}{\sqrt{2}}
. С другой стороны, так как
\angle AEC=\angle AEB=90^{\circ},
то
\frac{1}{\sqrt{2}}=k=\frac{CE}{AC}=\cos\angle ACE=\cos\gamma.
Поэтому \gamma=45^{\circ}
.
Пусть прямая DE
пересекается с прямой AB
в точке K
. По условию \angle AKD=15^{\circ}
. В то же время, ABC
— внешний угол треугольника BEK
, поэтому
\angle ABC=\angle AKD+\angle BEK=\angle AKD+\angle CED,~\mbox{или}~\beta=15^{\circ}+\alpha.
Подставив \beta
в равенство
\alpha+\beta=180^{\circ}-45^{\circ}=135^{\circ},
найдём, что \alpha=60^{\circ}
. Следовательно, \beta=75^{\circ}
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1993, № 5, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.14, с. 123
