2761. В остроугольном треугольнике ABC
проведены высоты CH
и AH_{1}
. Известно, что AC=2
, площадь круга, описанного около треугольника HBH_{1}
, равна \frac{\pi}{3}
. Найдите угол между высотой CH
и стороной BC
.
Ответ. 30^{\circ}
.
Указание. Треугольник BH_{1}H
подобен треугольнику BAC
с коэффициентом \cos\angle B
.
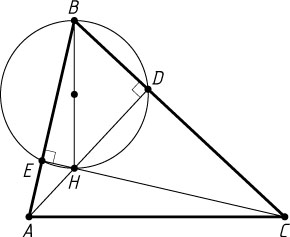
Решение. Первый способ. Пусть P
— точка пересечения высот треугольника ABC
. Из точек H
и H_{1}
отрезок BP
виден под прямым углом, значит, эти точки лежат на окружности с диаметром BP
. Пусть радиус этой окружности равен R
. Тогда \pi R^{2}=\frac{\pi}{3}
. Отсюда находим, что R=\frac{1}{\sqrt{3}}
.
По теореме синусов HH_{1}=2R\sin\angle B=\frac{2}{\sqrt{3}}\sin\angle B
. С другой стороны, треугольник BH_{1}H
подобен треугольнику BAC
с коэффициентом \cos\angle B
(см. задачу 19), поэтому HH_{1}=AC\cos\angle B=2\cos\angle B
.
Из равенства \frac{2}{\sqrt{3}}\sin\angle B=2\cos\angle B
находим, что \tg\angle B=\sqrt{3}
. Значит, \angle B=60^{\circ}
. Следовательно,
\angle BCH=90^{\circ}-\angle CBH=90^{\circ}-\angle B=90^{\circ}-60^{\circ}=30^{\circ}.
Второй способ. Пусть P
— точка пересечения высот треугольника ABC
. Из точек H
и H_{1}
отрезок BP
виден под прямым углом, значит, эти точки лежат на окружности с диаметром BP
. Пусть радиус этой окружности равен R
. Тогда \pi R^{2}=\frac{\pi}{3}
. Отсюда находим, что R=\frac{1}{\sqrt{3}}
.
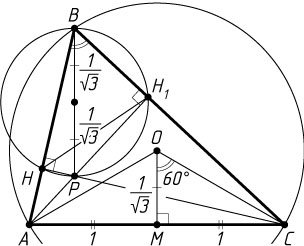
Пусть O
— центр окружности, описанной около треугольника ABC
, M
— середина стороны AC
. Расстояние от точки O
до стороны AC
вдвое меньше расстояния от точки P
пересечения высот до вершины B
(см. задачу 1257), а так как BP=\frac{2}{\sqrt{3}}
, то OM=\frac{1}{\sqrt{3}}
. Из прямоугольного треугольника OMC
находим, что \tg\angle MOC=\frac{MC}{OM}=\sqrt{3}
, значит, \angle MOC=60^{\circ}
.
По теореме о вписанном угле
\angle ABC=\frac{1}{2}\angle AOC=\angle MOC=60^{\circ}.
Следовательно,
\angle BCH=90^{\circ}-\angle CBH=90^{\circ}-\angle ABC=90^{\circ}-60^{\circ}=30^{\circ}.
Источник: Вступительный экзамен на факультет психологии МГУ. — 1993, № 4, вариант 2
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 15.24.1, с. 162

