2984. Окружность, касающаяся сторон AC
и BC
треугольника ABC
в точках M
и N
, касается также внутренним образом его описанной окружности (полувписанная окружность). Докажите, что середина отрезка MN
совпадает с центром вписанной окружности треугольника ABC
.
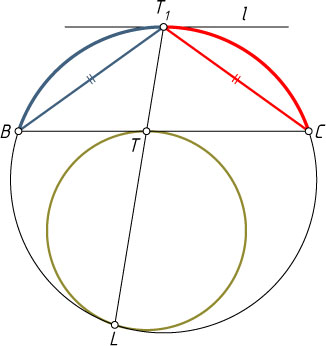
Решение. Первый способ. Лемма 1. Две окружности касаются внутренним образом в точке L
. Пусть BC
— хорда большей окружности, касающаяся меньшей окружности в точке T
. Тогда луч LT
проходит через середину дуги BC
, не содержащей точки L
.
Доказательство. При гомотетии с центром L
, переводящей меньшую окружность в большую, касательная BC
к меньшей окружности переходит в параллельную ей касательную l
к большей окружности (рис. 1). Точка касания T
переходит в точку касания T_{1}
прямой l
с большей окружностью. Тогда точки L
, T
и T_{1}
лежат на одной прямой, причём T_{1}
— середина дуги BC
, так как T_{1}B=T_{1}C
. Лемма доказана.
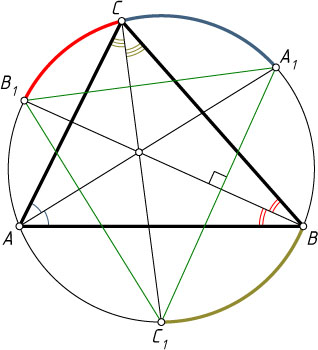
Лемма 2. Продолжения биссектрис остроугольного треугольника ABC
пересекают описанную окружность в точках A_{1}
, B_{1}
и C_{1}
соответственно. Тогда высоты треугольника A_{1}B_{1}C_{1}
лежат на прямых AA_{1}
, BB_{1}
и CC_{1}
.
Доказательство. Обозначим углы треугольника ABC
через \alpha
, \beta
и \gamma
соответственно.
Угол между хордами BB_{1}
и C_{1}A_{1}
равен полусумме дуг BA_{1}
и C_{1}AB_{1}
(рис. 2) (см. задачу 26). Поскольку
\smile BA_{1}=2\angle BAA_{1}=\alpha,
\smile C_{1}AB_{1}=\smile C_{1}A+\smile AB_{1}=2\angle ACC_{1}+2\angle ABB_{1}=\gamma+\beta,
то
\frac{1}{2}(\smile BA_{1}+\smile C_{1}AB_{1})=\frac{1}{2}(\alpha+\beta+\gamma)=\frac{1}{2}\cdot180^{\circ}=90^{\circ}.
Следовательно, BB_{1}\perp C_{1}A_{1}
. Остальное аналогично. Лемма доказана.
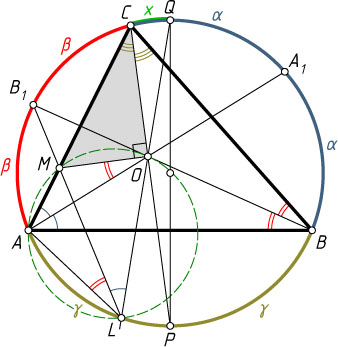
Лемма 3. Через точку O
пересечения биссектрис треугольника ABC
проведена прямая MN
перпендикулярно CO
, причём точки M
и N
лежат на сторонах AC
и BC
соответственно. Прямые AO
и BO
пересекают описанную окружность треугольника ABC
в точках A_{1}
и B_{1}
. Тогда точка пересечения прямых A_{1}N
и B_{1}M
лежит на описанной окружности.
Доказательство. Пусть луч CO
пересекает описанную окружность треугольника ABC
в точке P
(рис. 3). Проведём диаметр PQ
окружности ABC
, перпендикулярный AB
. Предположим, что AC\lt BC
. Пусть луч QO
пересекает окружность в точке L
, а отрезки LB_{1}
и AC
пересекаются в точке M_{1}
. Докажем, что OM_{1}\perp CO
.
Обозначим углы треугольника ABC
через \alpha
, \beta
и \gamma
соответственно, а дугу CQ
через x
. Центр O
вписанной окружности треугольника ABC
— точка пересечения его биссектрис, поэтому точки P
и B_{1}
— середины дуг AB
и AC
,
\smile AP=\gamma,~\smile AB_{1}=\smile B_{1}C=\beta,
значит,
\gamma+2\beta+x=180^{\circ},
откуда
x=180^{\circ}-\gamma-2\beta=\alpha+\beta-2\beta=\alpha-\beta.
Следовательно,
\angle QLB_{1}=\frac{1}{2}\smile B_{1}Q=\frac{1}{2}(\beta+x)=\frac{1}{2}(\beta+(\alpha-\beta))=\frac{\alpha}{2}=\angle M_{1}AO.
Из точек L
и A
, лежащих по одну сторону от прямой OM_{1}
, отрезок OM_{1}
виден под одним и тем же углом (\frac{\alpha}{2}
), значит, точки L
, A
, O
и M_{1}
лежат на одной окружности. Вписанные в эту окружность углы ALM_{1}
и AOM_{1}
опираются на одну и ту же дугу, поэтому
\angle AOM_{1}=\angle ALM_{1}=\angle ALB_{1}=\frac{1}{2}\smile AB_{1}=\frac{\beta}{2}.
По теореме о внешнем угле треугольника
\angle OM_{1}C=\angle OAM_{1}+\angle AOM_{1}=\frac{\alpha}{2}+\frac{\beta}{2},
поэтому
\angle COM_{1}=180^{\circ}-\angle OM_{1}C-\angle OCM_{1}=180^{\circ}-\left(\frac{\alpha}{2}+\frac{\beta}{2}\right)-\frac{\gamma}{2}=90^{\circ}.
Значит, OM_{1}\perp CO
.
Следовательно, точка M_{1}
совпадает с M
. Аналогично точка N_{1}
пересечения LA_{1}
и BC
совпадает с N
. Отсюда следует справедливость леммы.
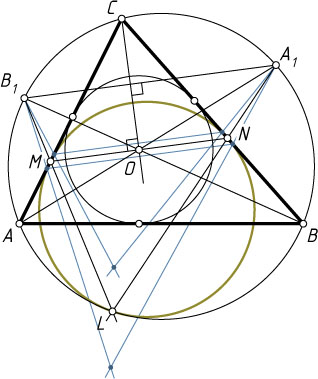
Перейдём к нашей задаче. Пусть O
— центр вписанной окружности треугольника ABC
, A_{1}
, B_{1}
и C_{1}
— точки пересечения продолжений биссектрис соответственно AO
, BO
и CO
с описанной окружностью. Тогда A_{1}
, B_{1}
и C_{1}
— середины дуг BC
, AC
и AB
. Пусть L
— точка касания окружности, касающейся сторон AC
и BC
треугольника ABC
соответственно в точках M
и N
, с описанной окружность этого треугольника. Тогда из леммы 1 следует, что прямые A_{1}N
и B_{1}M
пересекаются на описанной окружности треугольника ABC
.
Точка O
лежит на биссектрисе CC_{1}
угла ACB
, поэтому A_{1}B_{1}\perp OC
(лемма 2). Кроме того MN\perp OC
, так как биссектриса CO
равнобедренного треугольника CMN
является его высотой. Значит, MN\parallel A_{1}B_{1}
.
Будем перемещать точки M'
и N'
по лучам CA
и CB
так, что M'N'\parallel A_{1}B_{1}
. Лишь при одном положении точек M'
и N'
точка, в которой пересекаются прямые A_{1}N'
и B_{1}M'
, попадает на описанную окружность треугольника ABC
. Это точка L
, в которой окружность, вписанная в угол ACB
, касается описанной окружности треугольника ABC
.
В этом случае отрезок MN
проходит через центр O
вписанной окружности треугольника ABC
(лемма 3).
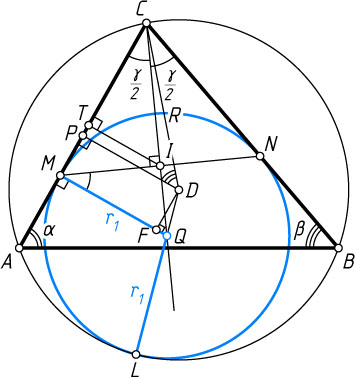
Второй способ. Пусть углы при вершинах A
, B
и C
треугольника ABC
равны \alpha
, \beta
и \gamma
соответственно (рис. 5), Q
— центр окружности радиуса r_{1}
, касающейся сторон AC
, BC
и описанной окружности радиуса R
с центром D
, P
— проекция точки D
на AC
, r
— радиус вписанной окружности треугольника ABC
, I
— точка пересечения биссектрисы угла ACB
с отрезком MN
, T
— проекция точки I
на AC
.
В равнобедренном треугольнике CMN
биссектриса CI
является высотой и медианой. Поскольку \angle QMI=\frac{\gamma}{2}
, из прямоугольных треугольников QIM
и ITM
находим, что
IM=QM\cos\frac{\gamma}{2}=r_{1}\cos\frac{\gamma}{2},~IT=IM\cos\frac{\gamma}{2}=r_{1}\cos^{2}\frac{\gamma}{2}.
Для доказательства утверждения достаточно установить, что IT=r
, или r_{1}\cos^{2}\frac{\gamma}{2}=r
.
Из прямоугольного треугольника CQM
находим, что
CM=r_{1}\ctg\frac{\gamma}{2}.
По теореме синусов
CP=\frac{b}{2}=\frac{1}{2}\cdot2R\sin\beta=R\sin\beta,
поэтому
MP=|CP-CM|=\left|R\sin\beta-r_{1}\ctg\frac{\gamma}{2}\right|.
Из прямоугольного треугольника CDP
находим, что
DP=DC\cos\angle CDP=R\cos\beta.
Линия центров касающихся окружностей проходит через их точку касания, поэтому
DQ=DL-QL=R-r_{1}.
Пусть F
— проекция точки D
на MQ
. Тогда
DF=MP=\left|R\sin\beta-r_{1}\ctg\frac{\gamma}{2}\right|,
QF=|QM-FM|=|QM-DP|=|r_{1}-R\cos\beta|.
Применив теорему Пифагора к треугольнику DFQ
, получим, что DQ^{2}=DF^{2}+QF^{2}
, или
(R-r_{1})^{2}=\left(R\sin\beta-r_{1}\ctg\frac{\gamma}{2}\right)^{2}+(r_{1}-R\cos\beta)^{2}.
Отсюда находим, что
r_{1}=2R\left(\frac{\sin\beta\ctg\frac{\gamma}{2}+\cos\beta}{\ctg^{2}\frac{\gamma}{2}}-1\right)=2R\left(\frac{\sin\beta\cos\frac{\gamma}{2}+\cos\beta\sin\frac{\gamma}{2}}{\ctg^{2}\frac{\gamma}{2}\sin\frac{\gamma}{2}}-1\right)=
=\frac{2R}{\ctg^{2}\frac{\gamma}{2}}\left(\frac{\sin\left(\beta+\frac{\gamma}{2}\right)}{\sin\frac{\gamma}{2}}-1\right)=\frac{2R}{\ctg^{2}\frac{\gamma}{2}\sin\frac{\gamma}{2}}\left(\sin\left(\beta+\frac{\gamma}{2}\right)-\sin\frac{\gamma}{2}\right)=
=\frac{2R}{\ctg^{2}\frac{\gamma}{2}\sin\frac{\gamma}{2}}\cdot2\sin\frac{\beta}{2}\cos\frac{\beta+\gamma}{2}=\frac{2R}{\ctg^{2}\frac{\gamma}{2}\sin\frac{\gamma}{2}}\cdot2\sin\frac{\beta}{2}\sin\frac{\alpha}{2}=
=\frac{4R\sin\frac{\beta}{2}\sin\frac{\gamma}{2}\sin\frac{\alpha}{2}}{\cos^{2}\frac{\gamma}{2}}=\frac{r}{\cos^{2}\frac{\gamma}{2}},
так как
4R\sin\frac{\beta}{2}\sin\frac{\gamma}{2}\sin\frac{\alpha}{2}=r
(см. задачу 3225). Следовательно, r_{1}\cos^{2}\frac{\gamma}{2}=r
. Что и требовалось доказать.
Третий способ. Пусть радиус окружности S
равен r_{1}
, радиус вписанной окружности треугольника ABC
равен r
, а \angle BAC=\alpha
. Точка I
— середина основания MN
равнобедренного треугольника MAN
, поэтому
AI=AN\cos\frac{\alpha}{2}=r_{1}\ctg\frac{\alpha}{2}\cdot\cos\frac{\alpha}{2}=\frac{r}{\cos^{2}\frac{\alpha}{2}}\cdot\ctg\frac{\alpha}{2}\cos\frac{\alpha}{2}=\frac{r}{\sin\frac{\alpha}{2}}
(см. задачу 11076).
С другой стороны, если I'
— центр вписанной окружности треугольника ABC
, то AI'=\frac{r}{\sin\frac{\alpha}{2}}=AI
. Значит, точки I
и I'
совпадают. Отсюда следует доказываемое утверждение.
Примечание. См. статью А.Гирича «Несколько задач о треугольниках и окружностях», Квант, 1990, N11, с.46-48.
Источник: Журнал «Квант». — 1990, № 11, с. 47, задача 3
Источник: Готман Э. Г. Задачи по планиметрии и методы их решения. — М.: Просвещение, 1996. — № 533, с. 135
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.45, с. 65
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.47, с. 62
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 340(б), с. 52




