3183. Пусть A_{1}
— точка, симметричная вершине A
треугольника ABC
относительно прямой BC
. Докажите, что прямая, проходящая через точку A
и центр описанной окружности треугольника A_{1}BC
, проходит через точку O_{9}
— центр окружности девяти точек треугольника ABC
.
Указание. Пусть O
— центр описанной окружности треугольника ABC
, H
— ортоцентр треугольника. Тогда центр окружности девяти точек треугольника ABC
— середина отрезка OH
(см. задачу 174).
Решение. Пусть H
— ортоцентр треугольника ABC
, O
— центр описанной окружности этого треугольника, O_{1}
— центр описанной окружности треугольника A_{1}BC
.
Известно, что центр окружности девяти точек треугольника ABC
— середина отрезка OH
(см. задачу 174). Значит, достаточно доказать, что прямая AO_{1}
делит пополам отрезок OH
.
Треугольники ABC
и A_{1}BC
симметричны относительно прямой BC
, поэтому центры O
и O_{1}
их описанных окружностей также симметричны относительно BC
. Пусть прямая AO_{1}
пересекает отрезок OH
в точке Q
, M
— середина BC
. Тогда OO_{1}=2OM=AH
(см. задачу 1257) и OO_{1}\parallel AH
, поэтому треугольники AHQ
и O_{1}OQ
равны по стороне и двум прилежащим к ней углам. Следовательно, QH=QO
, т. е. точка Q
совпадает с O_{9}
. Что и требовалось доказать.
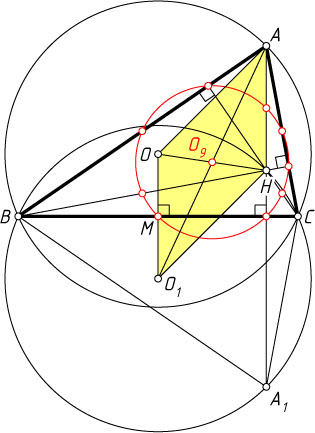
Источник: Журнал «Квант». — 2012, № 5-6, с. 59
