3262. На дуге AB
окружности возьмём произвольную точку P
и опустим перпендикуляры AG
и BH
на прямые BP
и AP
. Докажите, что прямая GH
касается некоторой фиксированной окружности.
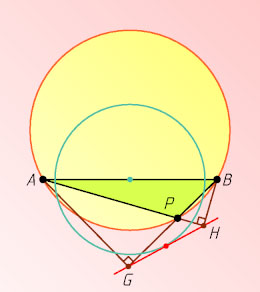
Указание. Точки G
и H
лежат на окружности с диаметром AB
, а все хорды GH
этой окружности равны.
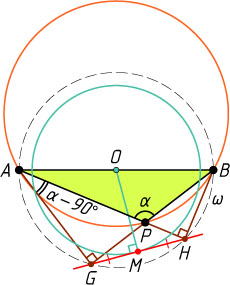
Решение. Из точек G
и H
отрезок AB
виден под прямым углом, значит эти точки лежат на окружности \omega
с диаметром AB
и с центром в середине O
отрезка AB
. Хорда GH
этой окружности видна из точки A
под фиксированным углом \angle APB-90^{\circ}
, так как APB
— внешний угол прямоугольного треугольника APG
, а из каждой точки дуги AB
отрезок AB
виден под одним и тем же углом. Поэтому все хорды GH
равны (см. задачу 805), а значит, они равноудалены от центра O
окружности \omega
. Если M
— середина хорды GH
, то OM\perp GH
. Следовательно, все прямые GH
касаются окружности с центром O
и постоянным радиусом, равным OM
(см. задачу 1735).
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 43, с. 34

