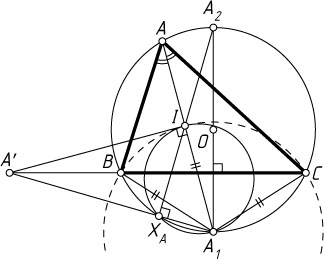
3275. Пусть I
— центр вписанной окружности неравнобедренного треугольника ABC
. Через A_{1}
обозначим середину дуги BC
описанной окружности треугольника ABC
, не содержащей точки A
, а через A_{2}
— середину дуги BAC
. Перпендикуляр, опущенный из точки A_{1}
на прямую A_{2}I
, пересекает прямую BC
в точке A'
. Аналогично определяются точки B'
и C'
.
а) Докажите, что точки A'
, B'
и C'
лежат на одной прямой.
б) Докажите, что эта прямая перпендикулярна прямой OI
, где O
— центр описанной окружности треугольника ABC
.
Указание. Пусть X_{A}
— точка пересечения прямых A_{1}A'
и A_{2}I
. Примените теорему о радикальном центре трёх окружностей (см. задачу 6393) к описанным окружностям треугольников ABC
, BIC
и IX_{A}A_{1}
.
Решение. Обозначим точку пересечения прямой A_{1}A'
с прямой A_{2}I
через X_{A}
, а описанную окружность треугольника ABC
через \omega
. Из условия следует, что \angle A_{2}X_{A}A_{1}=90^{\circ}
, поскольку A_{2}A_{1}
— диаметр \omega
, а точка X_{A}
лежит на \omega
.
Рассмотрим теперь описанные окружности треугольников ABC
, BIC
и IX_{A}A_{1}
. Радикальная ось первой и второй окружностей есть прямая BC
, а первой и третьей — X_{A}A_{1}
, так как это прямые, содержащие общие хорды этих окружностей (см. задачу 6391). Значит, радикальным центром всех этих трёх окружностей является точка A'
(см. задачу 6393).
Заметим, что A_{1}I=A_{1}B=A_{1}C
(см. задачу 788), поэтому точка A_{1}
— центр описанной окружности треугольника BIC
, а так как угол IX_{A}A_{1}
прямой, то IA_{1}
— диаметр описанной окружности треугольника A_{1}IX_{A}
. Следовательно, описанные окружности треугольников BIC
и X_{A}IA_{1}
касаются в точке I
. Значит, общая касательная к этим окружностям, проведённая в точке I
(т. е. радикальная ось этих окружностей), проходит через A'
. При этом, по теореме о касательной и секущей, проведённых из точки A'
к описанной окружности треугольника BIC
, верно равенство A'I^{2}=A'B\cdot A'C
.
Рассмотрим \omega
и точку I
как вырожденную в точку окружность. Из последнего равенства следует, что точка A'
лежит на радикальной оси этих двух окружностей. Аналогично на этой радикальной оси лежат и точки B'
и C'
. Поскольку радикальная ось двух окружностей — прямая, все эти три точки лежат на одной прямой, перпендикулярной линии центров этих окружностей, т. е. на прямой OI
. Что и требовалось доказать.
Автор: Ивлев Ф. А.
Источник: Московская математическая олимпиада. — 2013, LXXVI, 10 класс
