3285. Точка E
расположена вне квадрата ABCD
с центром O
, причём треугольник BEC
прямоугольный (\angle E=90^{\circ}
) и неравнобедренный. Точка M
— середина стороны BC
.
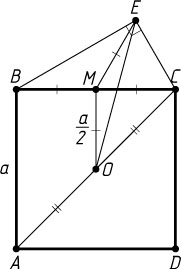
а) Докажите, что треугольник OME
равнобедренный.
б) Прямая EO
пересекает сторону AD
квадрата в точке K
. Найдите отношение AK:KD
, если известно, что \angle CBE=30^{\circ}
.
Ответ. \sqrt{3}:3
.
Указание. Точки O
, B
, C
и E
лежат на одной окружности.
Решение. а) Отрезок EM
— медиана прямоугольного треугольника BEC
, проведённая из вершины прямого угла (рис. 1), поэтому EM=\frac{1}{2}BC=\frac{1}{2}AB
(см. задачу 1109). Отрезок OM
— средняя линия треугольника ABC
, поэтому MO=\frac{1}{2}AB
. Значит, EM=MO
. Следовательно, треугольник OME
равнобедренный.
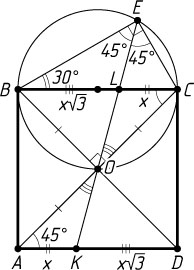
б) Из точек E
и O
отрезок BC
виден под прямым углом, значит, эти точки лежат на окружности с диаметром BC
(рис. 2). Вписанные в эту окружность углы BEO
и CEO
опираются на равные хорды OB
и OC
, поэтому EO
— биссектриса угла BEC
.
Пусть L
— точка пересечения отрезков EO
и BC
. Тогда EL
— биссектриса треугольника BEC
. По свойству биссектрисы треугольника (см. задачу 1509)
\frac{CL}{LB}=\frac{CE}{BE}=\tg\angle CBE=\tg30^{\circ}=\frac{1}{\sqrt{3}}.
Треугольник AOK
равен треугольнику COL
по стороне и прилежащим к ней углам, поэтому AK=CL
. Аналогично KD=LB
. Следовательно,
\frac{AK}{KD}=\frac{CL}{LB}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 1.31, с. 13
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1.31.1, с. 13

