3455. Окружность с центром O
, вписанная в треугольник ABC
, касается стороны BC
в точке M
. Окружность с центром O_{1}
касается стороны BC
в точке N
, а также касается продолжений сторон AC
и AB
.
а) Докажите, что около четырёхугольника BOCO_{1}
можно описать окружность.
б) Найдите площади четырёхугольников BOCO_{1}
и NOMO_{1}
, если известно, что AC=6
, BC=8
, AB=10
.
Ответ. 32 и 16.
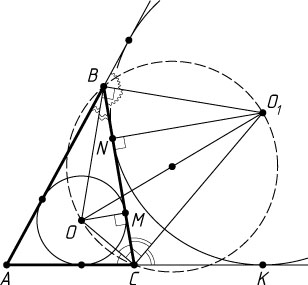
Решение. а) Пусть окружность с центром O_{1}
касается продолжения стороны AC
в точке K
(рис. 1). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому CO
и CO_{1}
— биссектрисы углов ACB
и KCB
. Значит, \angle OCO_{1}=90^{\circ}
как угол между биссектрисами смежных углов. Аналогично \angle OBO_{1}=90^{\circ}
. Из точек C
и B
отрезок OO_{1}
виден под прямым углом, следовательно, эти точки лежат на окружности с диаметром OO_{1}
.
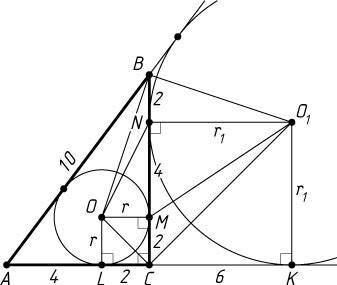
б) Треугольник ABC
прямоугольный, так как AB^{2}=100=36+64=AC^{2}+BC^{2}
(рис. 2). Пусть r
и r_{1}
— радиусы рассматриваемых окружностей с центрами O
и O_{1}
соответственно, а окружность с центром O
касается катета AC
в точке L
. Тогда OMCL
и O_{1}KCN
— квадраты со сторонами r
и r_{1}
соответственно. Значит,
r=OM=CL=p-AB=12-10=2,~r_{1}=AK-AC=p-6=6
(см. задачи 219 и 4805), где p=\frac{AB+BC+AC}{2}=\frac{10+8+6}{2}=12
— полупериметр треугольника ABC
. Следовательно,
S_{BOCO_{1}}=S_{\triangle BOC}+S_{\triangle BO_{1}C}=\frac{1}{2}BC\cdot OM+\frac{1}{2}BC\cdot O_{1}N=
=\frac{1}{2}BC(OM+O_{1}N)=\frac{1}{2}\cdot8\cdot8=32.
Поскольку
BN=p-AC=12-10=2,~MN=8-2-2=4,
аналогично находим, что
S_{NOMO_{1}}=\frac{1}{2}MN(r+r_{1})=\frac{1}{2}\cdot4\cdot8=16.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 8.36, с. 77
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 8.36.1, с. 84

