3482. Точки A_{1}
, B_{1}
и C_{1}
— основания высот треугольника ABC
, O
— центр его описанной окружности.
а) Докажите, что OA\perp B_{1}C_{1}
.
б) Найдите площадь треугольника ABC
, если известно, что A_{1}B_{1}=21
, A_{1}C_{1}=17
, B_{1}C_{1}=10
.
Ответ. 510.
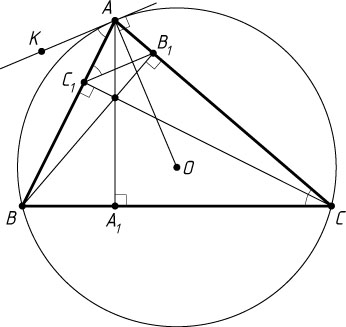
Решение. а) Пусть KA
— касательная к описанной окружности треугольника ABC
(рис. 1), причём точки K
и C
лежат по разные стороны от прямой AB
. Поскольку BB_{1}
и CC_{1}
— высоты треугольника ABC
, то \angle AC_{1}B_{1}=\angle ACB
. Из теоремы об угле между касательной и хордой следует, что \angle KAB=\angle ACB
, значит, \angle AC_{1}B_{1}=\angle KAB
. Поэтому B_{1}C_{1}\parallel AK
, а так как OA\perp AK
, то OA\perp B_{1}C_{1}
.
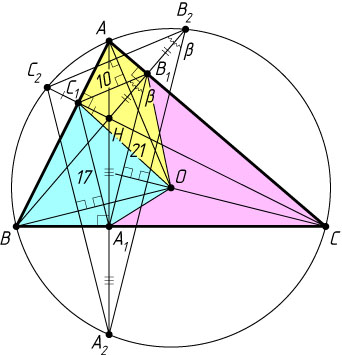
б) Аналогично OB\perp A_{1}C_{1}
и OC\perp A_{1}B_{1}
(рис. 2). Пусть H
— точка пересечения высот треугольника ABC
. Продолжим высоты AA_{1}
, BB_{1}
и CC_{1}
до пересечения с описанной окружностью треугольника ABC
в точках A_{2}
, B_{2}
и C_{2}
соответственно. Тогда A_{1}
, B_{1}
, C_{1}
— середины отрезков HA_{2}
, HB_{2}
и HC_{2}
(см. 4785), значит, B_{1}C_{1}
, A_{1}C_{1}
и A_{1}B_{1}
— средние линии треугольников B_{2}HC_{2}
, A_{2}HC_{2}
и A_{2}HB_{2}
. Поэтому треугольник A_{2}B_{2}C_{2}
подобен треугольнику A_{1}B_{1}C_{1}
с коэффициентом 2.
Обозначим \angle A_{2}B_{2}C_{2}=\angle A_{1}B_{1}C_{1}=\beta
. По теореме косинусов находим, что
\cos\beta=\frac{10^{2}+21^{2}-17^{2}}{2\cdot10\cdot21}=\frac{3}{5}.
Тогда \sin\beta=\frac{4}{5}
.
Пусть R
— радиус описанной окружности треугольника ABC
. По теореме синусов
R=\frac{A_{2}C_{2}}{2\sin\beta}=\frac{34}{2\cdot\frac{4}{5}}=\frac{85}{4}.
Площадь треугольника ABC
равна сумме площадей четырёхугольников AB_{1}OC_{1}
, BA_{1}OC_{1}
и CB_{1}OA_{1}
, диагонали каждого из которых перпендикулярны. Следовательно,
S_{\triangle ABC}=\frac{1}{2}OA\cdot B_{1}C_{1}+\frac{1}{2}OB\cdot A_{1}C_{1}+\frac{1}{2}OC\cdot A_{1}B_{1}=
=\frac{1}{2}R\cdot10+\frac{1}{2}R\cdot17+\frac{1}{2}R\cdot21=\frac{1}{2}R(10+17+21)=\frac{1}{2}\cdot\frac{85}{4}\cdot48=510.
Примечание. Можно применить готовую формулу для площади треугольника S=Rq
(см. примечание к задаче 4305), где R
— радиус описанной окружности треугольника, а q
— полупериметр его ортотреугольника.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 15.28, с. 152
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 15.27.1, с. 162

