4305. Пусть p
— полупериметр остроугольного треугольника, R
и r
— радиусы соответственно описанной и вписанной окружностей, q
— полупериметр треугольника с вершинами в основаниях высот данного. Докажите, что R:r=p:q
.
Указание. Если BB'
и CC'
— высоты треугольника ABC
, а O
— центр описанной окружности, то OA\perp B'C'
(см. задачу 480).
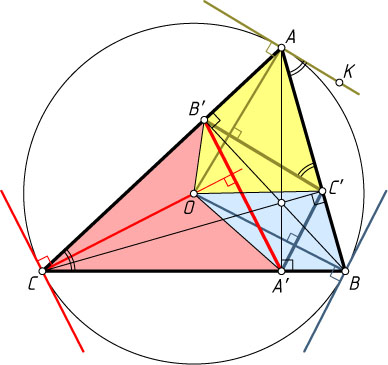
Решение. Первый способ. Пусть AA'
, BB'
и CC'
— высоты данного остроугольного треугольника (рис. 1), O
— центр его описанной окружности. Обозначим
BC=a,~AC=b,~AB=c,~B'C'=a',~A'C'=b',~A'B'=c'.
Воспользуемся известным фактом: \angle ACB=\angle AC'B'
(см. задачу 141). На касательной к описанной окружности треугольника ABC
, проведённой через вершину A
, возьмём точку K
так, чтобы эта точка и вершина C
лежали по разные стороны от прямой AB
. Из теоремы об угле между касательной и хордой следует, что
\angle BAK=\angle ACB=\angle AC'B'.
Значит, AK\parallel B'C'
, а так как OA\perp AK
, то OA\perp B'C'
. Аналогично докажем, что OB\perp A'C'
и OC\perp A'B'
.
У каждого из четырёхугольников AB'OC'
, BA'OC'
и CA'OB'
диагонали взаимно перпендикулярны, поэтому
pr=S_{\triangle ABC}=S_{AB'OC'}+S_{BA'OC'}+S_{CA'OB'}=
=\frac{1}{2}\cdot AO\cdot B'C'+\frac{1}{2}\cdot BO\cdot A'C'+\frac{1}{2}\cdot CO\cdot A'B'=
=\frac{1}{2}R(B'C'+A'C'+A'B')=\frac{1}{2}R(a'+b'+c')=Rq.
Следовательно, R:r=p:q
.
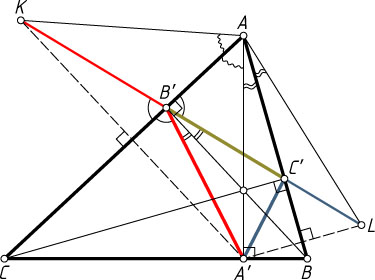
Второй способ. Пусть AA'
, BB'
и CC'
— высоты данного остроугольного треугольника (рис. 2). Обозначим
B'C'=a',~A'C'=b',A'B'=c',~\angle BAC=\alpha.
Воспользуемся известным фактом: высоты остроугольного треугольника делят пополам углы его ортотреугольника (см. задачу 533).
Пусть K
и L
— образы точки A'
при симметрии относительно прямых AC
и AB
соответственно (рис. 2). Тогда
\angle KB'C=\angle A'B'C=90^{\circ}-\angle A'B'B=90^{\circ}-\angle BB'C'=\angle AB'C'.
Значит, точка K
лежит на прямой B'C'
. Аналогично докажем, что точка L
также лежит на прямой B'C'
. Поэтому
KL=KB'+B'C'+C'L=A'B'+B'C'+A'C'=c'+a'+b'=2q.
Поскольку
AL=AA'=AK,~\angle LAB=\angle A'AB,~\angle KAC=\angle A'AC,
то \angle KAL=2\angle BAC=2\alpha
. Поэтому
2q=LK=2AK\cdot\sin\frac{1}{2}\angle KAL=2AA'\cdot\sin\alpha=
=2\cdot\frac{2S_{\triangle ABC}}{BC}\cdot\sin\alpha=2\cdot\frac{2pr}{2R\sin\alpha}\cdot\sin\alpha=\frac{2pr}{R}.
Следовательно, R:r=p:q
.
Примечание. Следствие: площадь треугольника равна произведению радиуса описанной окружности на полупериметр ортотреугольника (S=pr=Rq
).
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 75, с. 187
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 1.60, с. 18

