3895. В треугольнике ABC
известно, что AB=c
, AC=b
(b\gt c)
, AD
— биссектриса. Через точку D
проведена прямая, перпендикулярная AD
и пересекающая AC
в точке E
. Найдите AE
.
Ответ. \frac{2bc}{b+c}
.
Указание. Соедините точку D
с серединой отрезка AE
.
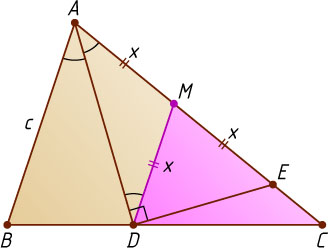
Решение. Пусть M
— середина отрезка AE
. Тогда DM
— медиана прямоугольного треугольника ADE
, проведённая из вершины прямого угла. Если DM=x
, то AM=ME=DM=x
, \angle ADM=\angle DAM=\angle BAD
(см. задачу 1109). Значит, DM\parallel AB
и треугольник MDC
подобен треугольнику ABC
, поэтому \frac{MD}{AB}=\frac{CM}{AC}
(см. задачу 1509), или \frac{x}{c}=\frac{b-x}{b}
, откуда находим, что x=\frac{bc}{b+c}
. Следовательно, AE=2x=\frac{2bc}{b+c}
.
Источник: Вступительный экзамен на физический факультет МГУ. — 1998 (май), вариант 1, № 8
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 1.21, с. 12
