3913. В треугольнике KLM
проведена биссектриса KP
. Окружность, вписанная в треугольник KLP
, касается стороны KL
в точке Q
, причём LQ=a
. На сторонах KL
и LM
выбраны точки E
и R
соответственно так, что прямая ER
проходит через центр окружности, вписанной в треугольник KLM
. Найдите длину биссектрисы KP
, если известно, что EL+LR=b
, а отношение площадей треугольников KLP
и ELR
равно \alpha
.
Ответ. \alpha b-2a
.
Указание. Если стороны треугольника равны p
и q
, а угол между ними равен \gamma
, то биссектрису c
треугольника, проведённую из вершины этого этого угла можно вычислить по формуле c=\frac{2pq\cos\frac{\gamma}{2}}{p+q}
.
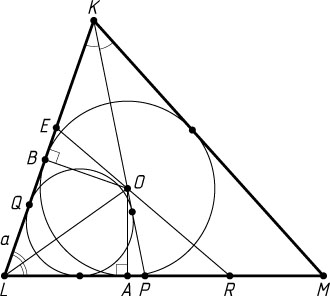
Решение. Первый способ. Пусть O
— центр окружности радиуса r
, вписанной в треугольник KLM
, A
и B
— её точки касания со сторонами LM
и KL
соответственно. Тогда
S_{\triangle KLP}=\frac{1}{2}LP\cdot OA+\frac{1}{2}KL\cdot OB=\frac{1}{2}(LP+KL)r,
S_{\triangle ELR}=\frac{1}{2}LR\cdot OA+\frac{1}{2}LE\cdot OB=\frac{1}{2}(LR+LE)r=\frac{1}{2}br,
а так как
\frac{S_{\triangle KLP}}{S_{\triangle ELR}}=\frac{LP+KL}{b}=\alpha,
то LP+KL=\alpha b
.
Пусть p
— полупериметр треугольника KLP
. Окружность, вписанная в треугольник KLP
касается стороны KL
в точке Q
, поэтому
a=LQ=p-KP=\frac{LP+KL-KP}{2}=\frac{\alpha b-KP}{2}
(см. задачу 219), откуда находим, что KP=\alpha b-2a
.
Второй способ. Пусть O
— центр окружности, вписанной в треугольник KLM
. Тогда LO
— биссектриса треугольников KLP
и ELR
. Обозначим \angle KLM=\gamma
. По формуле для биссектрисы треугольника (см. задачу 4021)
LO=\frac{2\cdot LE\cdot LR\cdot\cos\frac{\gamma}{2}}{LE+LR}~\mbox{и}~LO=\frac{2\cdot LK\cdot LP\cdot\cos\frac{\gamma}{2}}{LK+LP}.
Поэтому
\frac{LK\cdot LP}{LK+LP}=\frac{LE\cdot LR}{LE+LR}=\frac{LE\cdot LR}{b}~\Rightarrow~LK+LP=b\cdot\frac{LK\cdot LP}{LE\cdot LR},
а так как
\frac{S_{\triangle KLP}}{S_{\triangle ELR}}=\frac{\frac{1}{2}\cdot LK\cdot LP\cdot\sin\gamma}{\frac{1}{2}\cdot LE\cdot LR\cdot\sin\gamma}=\frac{LK\cdot LP}{LE\cdot LR}=\alpha,
то LK+LP=\alpha b
.
Из равенства отрезков касательных, проведённых к окружности из одной точки, следует, что KP=LK+LP-2\cdot LQ=\alpha b-2a
.
Источник: Вступительный экзамен на факультет психологии МГУ. — 1998, вариант 2, № 5
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.25, с. 41
