4306. Из вершины A
квадрата ABCD
со стороной 1 проведены два луча, пересекающие квадрат так, что вершина C
лежит между лучами. Угол между лучами равен \theta
. Из вершин B
и D
проведены перпендикуляры к лучам. Найдите площадь четырёхугольника с вершинами в основаниях этих перпендикуляров.
Ответ. \frac{1}{2}\sin^{2}\theta
.
Указание. Примените формулы тригонометрии.
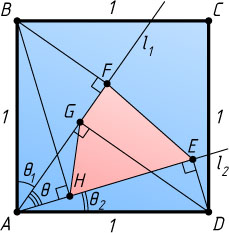
Решение. Первый способ. Пусть l_{1}
и l_{2}
— данные лучи, причём луч l_{1}
лежит между лучами AB
и l_{2}
, а луч l_{2}
— между лучами l_{1}
и AD
; G
и E
— проекции точки D
на лучи соответственно l_{1}
и l_{2}
, а F
и H
— проекции точки B
на эти лучи. Обозначим \angle BAF=\theta_{1}
, \angle DAE=\theta_{2}
. Тогда
S_{\triangle AEF}=\frac{1}{2}AE\cdot AF\sin\theta=\frac{1}{2}\sin\theta\cos\theta_{1}\cos\theta_{2},
S_{\triangle AGH}=\frac{1}{2}AG\cdot AH\sin\theta=\frac{1}{2}\sin\theta\sin\theta_{1}\sin\theta_{2}.
Следовательно,
S_{EFGH}=S_{\triangle AEF}-S_{\triangle AGH}=\frac{1}{2}\sin\theta\,(\cos\theta_{1}\cos\theta_{2}-\sin\theta_{1}\sin\theta_{2})=
=\frac{1}{2}\sin\theta\cos(\theta_{1}+\theta_{2})=\frac{1}{2}\sin\theta\cos(90^{\circ}-\theta)=\frac{1}{2}\sin^{2}\theta.
Второй способ. Пусть l_{1}
и l_{2}
— данные лучи, причём луч l_{1}
лежит между лучами AB
и l_{2}
, а луч l_{2}
— между лучами l_{1}
и AD
; G
и E
— проекции точки D
на лучи соответственно l_{1}
и l_{2}
, а F
и H
— проекции точки B
на эти лучи.
Точки F
и H
лежат на окружности с диаметром AB
, поэтому (см. задачу 23)
FH=AB\sin\angle FAH=\sin\theta.
Аналогично EG=\sin\theta
.
Острые углы с соответственно перпендикулярными сторонами равны, поэтому
\angle BHF=\angle BAF=\angle ADG=\angle AEG.
Стороны HB
и EA
равных углов BHF
и AEG
перпендикулярны, значит, стороны HF
и EG
также перпендикулярны. Следовательно (см. задачу 3018),
S_{FEHG}=\frac{1}{2}FH\cdot EG\sin90^{\circ}=\frac{1}{2}\sin^{2}\theta.
Источник: Турнир городов. — 1987-1988, IX, осенний тур, старшие классы, основной вариант
