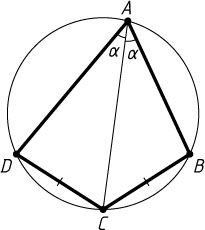
4336. Во вписанном четырёхугольнике ABCD
длины сторон BC
и CD
равны. Докажите, что площадь этого четырёхугольника равна \frac{1}{2}AC^{2}\sin\angle A
.
Решение. Первый способ. Обозначим \angle BAC=\alpha
. Поскольку хорды BC
и CD
равны, то равны дуги BC
и CD
, не содержащие точку A
. Поэтому
\angle DAC=\angle BAC=\alpha,~\angle BAD=2\alpha.
По теореме косинусов
BC^{2}=AB^{2}+AC^{2}-2AB\cdot AC\cos\alpha,~CD^{2}=AD^{2}+AC^{2}-2AD\cdot AC\cos\alpha.
Из равенства BC=CD
следует, что
AB^{2}+AC^{2}-2AB\cdot AC\cos\alpha=AD^{2}+AC^{2}-2AD\cdot AC\cos\alpha,
откуда находим, что
AB+AD=2AC\cos\alpha.
Следовательно,
S_{ABCD}=S_{\triangle ABC}+S_{\triangle ADC}=\frac{1}{2}AB\cdot AC\sin\alpha+\frac{1}{2}AD\cdot AC\sin\alpha=
=\frac{1}{2}AC(AB+AD)\sin\alpha=\frac{1}{2}AC\cdot2AC\cos\alpha\sin\alpha=\frac{1}{2}AC^{2}\sin2\alpha=\frac{1}{2}AC^{2}\sin\angle A.
Второй способ. Обозначим \angle BAC=\alpha
. Пусть E
— точка, симметричная вершине D
относительно серединного перпендикуляра к хорде AC
описанной окружности четырёхугольника ABCD
. Тогда точка E
лежит на этой окружности (см. задачу 1677), а так как
\angle ACE=\angle CAD=\angle BAC,
то AB\parallel CE
. Значит, ABCE
— равнобедренная трапеция. Угол между её диагоналями равен полусумме меньших дуг BC
и AE
(см. задачу 26), т. е. 2\alpha
. Треугольники AEC
и CDA
равны, следовательно
S_{ABCD}=S_{\triangle ABC}+S_{\triangle CDA}=S_{\triangle ABC}+S_{\triangle AEC}=
=S_{ABCE}=\frac{1}{2}AC^{2}\sin2\alpha=\frac{1}{2}AC^{2}\sin\angle A
(см. задачу 3018).
Автор: Фомин Д. В.
Источник: Турнир городов. — 1991-1992, XIII, осенний тур, старшие классы, основной вариант
