4358. В треугольнике ABC
проведены биссектрисы AD
и BE
. Известно, что DE
— биссектриса угла ADC
. Найдите величину угла A
.
Ответ. 120^{\circ}
.
Указание. Докажите, что E
— центр вневписанной окружности треугольника ADB
.
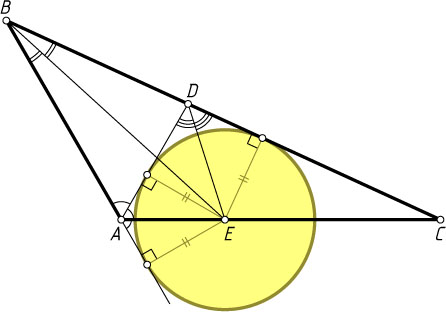
Решение. Первый способ. Точка E
равноудалена от прямых AD
, BC
и AB
, поскольку она лежит на биссектрисах DE
и BE
углов ADC
и ABC
(рис. 1). Значит, E
— центр вневписанной окружности треугольника ADB
. Поэтому точка E
лежит на биссектрисе внешнего угла при вершине A
треугольника ABD
, а так как AD
— биссектриса угла BAC
, то лучи AE
и AD
делят развёрнутый угол с вершиной A
на три равных угла. Следовательно, каждый из них равен 60^{\circ}
, а \angle BAC=120^{\circ}
.
Второй способ. Проведём через вершину B
прямую, параллельную AD
, до пересечения с прямой AC
в точке G
(рис. 2). Заметим, что
\angle GBA=\angle BAD=\angle DAE=\angle BGC,
т. е. треугольник BAG
равнобедренный (AB=AG
). Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам (см. задачу 1509). Применяя это свойство к биссектрисам DE
и BE
, получим, что DA:DC=AE:EC=BA:BC
. Но DA:DC=BG:BC
, так как треугольники ACD
и GCB
подобны. Значит, BA=BG
, и треугольник BAG
равносторонний. Следовательно, \angle BAG=60^{\circ}
, а \angle BAC=120^{\circ}
.
Примечание. Верно и обратное: если угол при вершине A
треугольника ABC
равен 120^{\circ}
, а AD
и BE
— биссектрисы треугольника, то DE
— биссектриса угла ADC
(см. задачу 1119).
Автор: Токарев С. И.
Источник: Турнир городов. — 1996-1997, XVIII, весенний тур, старшие классы, основной вариант
Источник: Международная олимпиада «Интеллектуальный марафон». — 2002, XI, письменный индивидуальный тур, задача 5
Источник: Журнал «Квант». — 2003, № 2, с. 54, задача 5
