4368. Дана трапеция ABCD
, M
— точка пересечения её диагоналей. Известно, что боковая сторона AB
перпендикулярна основаниям AD
и BC
и что в трапецию можно вписать окружность. Найдите площадь треугольника DCM
, если радиус этой окружности равен r
.
Ответ. r^{2}
.
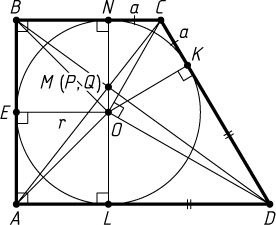
Решение. Первый способ. Пусть вписанная окружность с центром O
касается боковой стороны AB
в точке E
(рис. 1), основания BC
— в точке N
, боковой стороны CD
— в точке K
, основания AD
— в точке L
. Обозначим NC=CK=a
.
Отрезок OK
— высота прямоугольного треугольника COD
(см. задачу 313), проведённая из вершины прямого угла, поэтому
DK=\frac{OK^{2}}{CK}=\frac{r^{2}}{a}.
Пусть диаметр NL
вписанной в трапецию окружности пересекается с диагональю AC
в точке P
, а с диагональю BD
— в точке Q
. Из подобия треугольников PNC
и PLA
следует, что
\frac{NP}{PL}=\frac{NC}{LA}=\frac{a}{r},
а из подобия треугольников QNB
и QLD
—
\frac{NQ}{QL}=\frac{NB}{LD}=\frac{NB}{DK}=\frac{r}{\frac{r^{2}}{a}}=\frac{a}{r}.
Значит, \frac{NP}{PL}=\frac{NQ}{QL}
. Поэтому точки P
и Q
совпадают с точкой M
пересечения диагоналей трапеции, а точки O
и M
лежат на диаметре NL
, параллельном AB
. Следовательно (см. 4017),
S_{\triangle DCM}=S_{\triangle AMB}=S_{\triangle AOB}=\frac{1}{2}AB\cdot OE=\frac{1}{2}\cdot2r\cdot r=r^{2}.
Второй способ. Пусть вписанная окружность с центром O
касается боковой стороны AB
в точке E
(рис. 1), а оснований BC
и AD
— в точках N
и L
соответственно.
Отрезок NL
проходит через точку пересечения диагоналей (см. задачу 790), поэтому точки N
, M
, L
и O
лежат на одной прямой (параллельной AB
). Кроме того, треугольник CMB
равновелик треугольнику AMB
(см. 4017), который, в свою очередь, равновелик треугольнику AOB
. Следовательно,
S_{\triangle CMD}=S_{\triangle AMB}=S_{\triangle AOB}=\frac{1}{2}AB\cdot OE=\frac{1}{2}\cdot2r\cdot r=r^{2}.
Третий способ. Для решения задачи достаточно найти площадь треугольника ABM
. Она равна искомой (см. 4017).
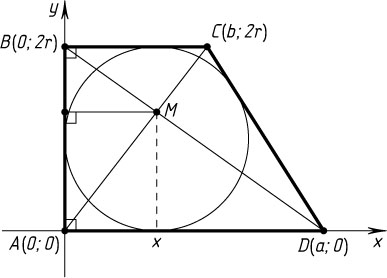
Введём декартову систему координат с началом в точке A
(рис. 2). Оси координат направим по лучам AD
и AB
(по условию AB\perp AD
). Тогда вершины трапеции имеют координаты: A(0;0)
, B(0;2r)
, C(b;2r)
, D(a;0)
.
Найдём абсциссу точки пересечения диагоналей M
, решив систему, составленную из уравнений диагоналей AC
: y=\frac{2r}{b}x
; BD
: y=-\frac{2r}{a}x+2r
. Абсцисса x
точки M
удовлетворяет уравнению
\frac{2r}{b}x=-\frac{2r}{a}x+2r,
откуда x=\frac{ab}{a+b}
.
Поскольку высота треугольника ABM
с основанием AB=2r
равна абсциссе точке M
, то
S_{\triangle AMB}=r\cdot\frac{ab}{a+b}.
Трапеция ABCD
— описанная, поэтому AB+CD=AD+BC
. По теореме Пифагора
CD=\sqrt{(a-b)^{2}+4r^{2}}.
Таким образом,
2r+\sqrt{(a-b)^{2}+4r^{2}}=a+b,
(a+b)^{2}-4r(a+b)+4r^{2}=(a-b)^{2}+4r^{2},
4r(a+b)=4ab,
r=\frac{ab}{a+b}.
Следовательно,
S_{\triangle DCM}=S_{\triangle AMB}=r^{2}.
Примечание. Тот факт, что диагонали трапеции пересекаются на диаметре NL
, следует из более общего утверждения: в любом описанном четырёхугольнике диагонали и отрезки, соединяющие точки касания вписанной окружности, лежащие на противоположных сторонах, пересекаются в одной точке (см. задачу 790).
Источник: Турнир городов. — 1986-1987, VIII, осенний тур, старшие классы, основной вариант

