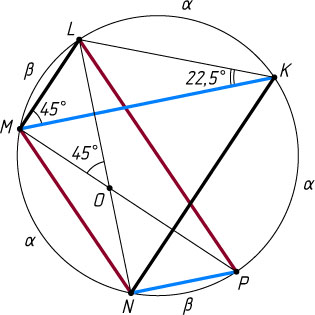
4760. Точки K
, L
, M
, N
, P
расположены последовательно на окружности радиуса 2\sqrt{2}
. Найдите площадь треугольника KLM
, если LM\parallel KN
, KM\parallel NP
, MN\parallel LP
, а угол LOM
равен 45^{\circ}
, где O
— точка пересечения хорд LN
и MP
.
Ответ. 4.
Указание. \angle LOM=\frac{\smile LM+\smile PN}{2}
.
Решение. Дуги, заключённые между параллельными хордами, равны, поэтому
\smile KL=\smile MN=\smile KP,~\smile LM=\smile PN.
Обозначим \smile KL=\alpha
, \smile LM=\beta
. Тогда
\angle LOM=\frac{\smile LM+\smile PN}{2}=\beta=45^{\circ},
\smile LK+\smile KP+\smile MN=3\alpha=360^{\circ}-2\beta=270^{\circ}
(см. задачу 26). Поэтому \alpha=90^{\circ}
. Следовательно,
\angle KML=\frac{\alpha}{2}=45^{\circ},~\angle LKM=\frac{\beta}{2}=22{,}5^{\circ}.
Если R
— радиус данной окружности, то
KL=2R\sin45^{\circ},~KM=2R\sin(180^{\circ}-45^{\circ}-22{,}5^{\circ})=2R\sin112{,}5^{\circ}=2R\cos22{,}5^{\circ}.
Следовательно,
S_{\triangle KLM}=\frac{1}{2}KL\cdot KM\sin22{,}5^{\circ}=
=\frac{1}{2}2R\sin45^{\circ}\cdot2R\cos22{,}5^{\circ}\cdot\sin22{,}5^{\circ}=R^{2}\sin45^{\circ}\sin45^{\circ}=4.
Примечание. Можно воспользоваться формулой для площади треугольника по радиусу описанной окружности и синусам трёх углов (см. задачу 4258).
Источник: Вступительный экзамен на факультет психологии МГУ. — 1992, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 617
