4804. В треугольник с периметром, равным 20, вписана окружность. Отрезок касательной, проведённый к окружности параллельно основанию, заключённый между сторонами треугольника, равен 2,4. Найдите основание треугольника.
Ответ. 6 или 4.
Указание. Отношение периметров подобных треугольников равно коэффициенту подобия.
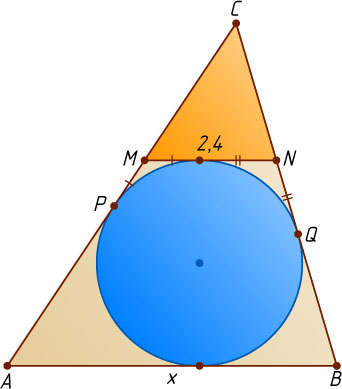
Решение. Обозначим точки пересечения касательной со сторонами AC
и CB
через M
и N
соответственно, а точки касания этих сторон с вписанной окружностью — соответственно через P
и Q
.
Обозначим AB=x
. Пусть p_{1}
и p
— полупериметры подобных треугольников CMN
и CAB
соответственно. Тогда CP=p_{1}
и CP=p-AB=p-x=10-x
(см. задачи 219 и 4805). Отношение полупериметров подобных треугольников равно коэффициенту подобия, поэтому \frac{p_{1}}{p}=\frac{MN}{AB}
, или \frac{10-x}{10}=\frac{2{,}4}{x}
. Из этого уравнения находим, что x=6
или x=4
.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.369, с. 183
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 6, задача 5
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5, с. 169
