4833. Найдите углы остроугольного треугольника ABC
, если известно, что его биссектриса AD
равна стороне AC
и перпендикулярна отрезку OH
, где O
— центр описанной окружности, H
— точка пересечения высот треугольника ABC
.
Ответ. 60^{\circ}
, 45^{\circ}
, 75^{\circ}
.
Указание. См. задачи 20 и 1257.
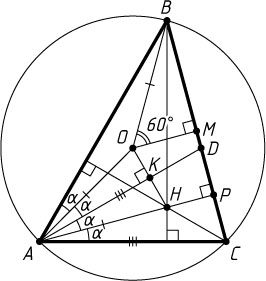
Решение. Обозначим \angle OAB=\alpha
. Пусть K
— точка пересечения AD
и OH
. Поскольку \angle OAB=\angle HAC
(см. задачу 20) и AD
— биссектриса угла BAC
, то AK
— биссектриса угла OAH
. По условию задачи эта биссектриса является высотой треугольника OAH
. Следовательно, треугольник OAH
— равнобедренный. Высота AP
равнобедренного треугольника CAD
является его биссектрисой, поэтому
\angle CAH=\angle KAH=\angle OAK=\angle OAB=\alpha.
Пусть M
— середина стороны BC
, а радиус описанной окружности треугольника ABC
равен R
. Тогда AH=OA=R
, а так как OM=\frac{1}{2}AH=\frac{1}{2}R
(см. задачу 1257), то из прямоугольного треугольника OBM
находим, что \angle BOM=60^{\circ}
. Вписанный угол BAC
равен половине центрального угла BOC
, т. е. 4\alpha=60^{\circ}
. Отсюда \alpha=15^{\circ}
. Тогда
\angle BAC=60^{\circ},~\angle ACB=90^{\circ}-\angle CAP=90^{\circ}-\alpha=75^{\circ},~\angle ABC=45^{\circ}.
Автор: Нистореску К. (Румыния)
Источник: Журнал «Квант». — 1990, № 4, с. 30, М1216
Источник: Задачник «Кванта». — М1216
