6030. Треугольник Наполеона. На сторонах произвольного треугольника внешним образом построены правильные треугольники. Докажите, что их центры образуют правильный треугольник.
Указание. Композиция поворотов на угол 120^{\circ}
вокруг центров соседних правильных треугольников есть поворот на угол (-120^{\circ})
вокруг центра третьего правильного треугольника. Воспользуйтесь также способом построения центра поворота, являющегося композицией двух поворотов с разными центрами.
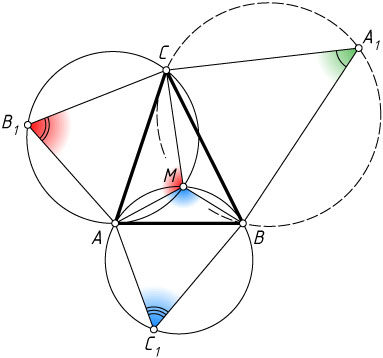
Решение. Первый способ. Пусть O_{1}
, O_{2}
и O_{3}
— центры указанных правильных треугольников A_{1}BC
, B_{1}AC
и C_{1}AB
, построенных на сторонах треугольника ABC
(рис. 1). Тогда
\angle BO_{1}C=\angle CO_{2}A=\angle AO_{3}B=120^{\circ}.
При композиции поворотов на 120^{\circ}
вокруг центров O_{1}
, O_{2}
, O_{3}
точка B
перейдёт в себя.
Поскольку сумма углов этих поворотов равна 360^{\circ}
, то такая композиция есть параллельный перенос (см. задачу 6710), а так как B
— неподвижная точка параллельного переноса, то это тождественное преобразование. Следовательно, композиция поворотов на 120^{\circ}
вокруг точек O_{1}
и O_{2}
есть поворот на угол (-120^{\circ})
вокруг точки O_{3}
.
С другой стороны, каждый из этих поворотов можно представить как композицию двух симметрий:
R^{120^{\circ}}_{O_{1}}=S_{l}\circ S_{a},~R^{120^{\circ}}_{O_{2}}=S_{b}\circ S_{l},
где l
— это прямая O_{1}O_{2}
, a
и b
— прямые, проходящие соответственно через точки O_{1}
и O_{2}
и образующие с прямой l
углы 60^{\circ}
и -60^{\circ}
.
Тогда прямые a
и b
пересекутся в центре поворота, являющегося композицией этих двух поворотов, т. е. в точке O_{3}
. Следовательно, треугольник O_{1}O_{2}O_{3}
— равносторонний.
Второй способ. Лемма 1. Если на сторонах треугольника ABC
внешним образом построены подобные треугольники AC_{1}B
, ACB_{1}
и A_{1}BC
, то описанные окружности построенных треугольников пересекаются в одной точке.
Доказательство. Обозначим через M
точку пересечения окружностей, описанных около треугольников AC_{1}B
и ACB_{1}
, отличную от A
, и докажем, что точка M
лежит на окружности, описанной около треугольника A_{1}BC
(рис. 2).
Поскольку углы при вершинах A_{1}
, B_{1}
, C_{1}
построенных треугольников не являются соответственными, их сумма равна 180^{\circ}
.
Пусть точка лежит внутри треугольника ABC
. Тогда
\angle BMC=360^{\circ}-\angle AMB-\angle AMC=
=360^{\circ}-(180^{\circ}-\angle AC_{1}B)-(180^{\circ}-\angle AB_{1}C)=\angle AC_{1}B+\angle AB_{1}C,
поэтому
\angle BMC+\angle BA_{1}C=\angle AC_{1}B+\angle AB_{1}C+\angle BA_{1}C=180^{\circ}.
Следовательно, точки B
, A_{1}
, M
, C
лежат на одной окружности, т. е. все три окружности проходят через точку M
. Аналогично для остальных случаев. Лемма доказана.
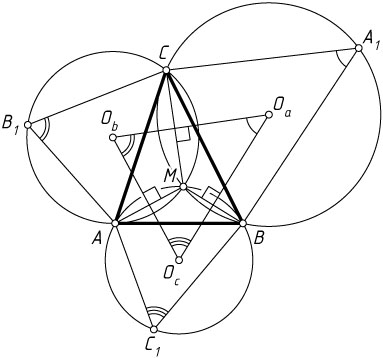
Лемма 2. Если сторонах треугольника ABC
внешним образом построены подобные треугольники AC_{1}B
, ACB_{1}
и A_{1}BC
, то центры их описанных окружностей являются вершинами треугольника, подобного трём построенным.
Доказательство. Пусть O_{c}
, O_{b}
и O_{a}
— центры описанных окружностей треугольников AC_{1}B
, ACB_{1}
и A_{1}BC
соответственно (рис. 3). По лемме 1 эти окружности имеют общую точку M
. Линия центров пересекающихся окружностей перпендикулярна их общей хорде, значит, O_{a}O_{c}\perp BM
и O_{a}O_{b}\perp CM
. Поэтому
\angle O_{b}O_{a}O_{c}=180^{\circ}-\angle BMC=\angle BA_{1}C.
Аналогично \angle O_{a}O_{b}O_{c}=\angle AB_{1}C=\angle CBA_{1}
. Следовательно, треугольник O_{a}O_{b}O_{c}
подобен треугольнику A_{1}BC
по двум углам. Лемма доказана.
Вернёмся к нашей задаче. Пусть AC_{1}B
, ACB_{1}
и A_{1}BC
— равносторонние треугольники. Тогда по лемме 1 треугольник O_{a}O_{b}O_{c}
подобен каждому из них. Следовательно, он равносторонний.
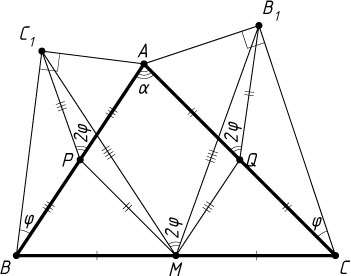
Третий способ. Лемма. Пусть на сторонах AB
и AC
треугольника ABC
внешним образом построены прямоугольные треугольники ABC_{1}
и AB_{1}C
, причём \angle C_{1}=\angle B_{1}=90^{\circ}
, \angle ABC_{1}=\angle ACB_{1}=\varphi
; M
— середина BC
. Тогда MB_{1}=MC_{1}
и \angle B_{1}MC_{1}=2\varphi
.
Доказательство. Пусть P
и Q
— середины сторон AB
и AC
соответственно (рис. 4). Тогда APMQ
— параллелограмм. Докажем, что треугольники MQB_{1}
и C_{1}PM
равны.
Действительно, B_{1}Q
и C_{1}P
— медианы прямоугольных треугольников AB_{1}C
и ABC_{1}
, поэтому (см. задачу 1109)
B_{1}Q=\frac{1}{2}AC=AQ=PM,~MQ=AP=\frac{1}{2}AB=C_{1}P,
\angle MQB_{1}=\angle MQA+\angle AQB_{1}=\angle MQA+2\varphi,
\angle C_{1}PM=\angle APM+\angle APC_{1}=\angle APM+2\varphi=\angle MQA+2\varphi=\angle MQB_{1}.
Значит, треугольники MQB_{1}
и C_{1}PM
равны по двум сторонам и углу между ними. Следовательно, MB_{1}=MC_{1}
.
Обозначим \angle BAC=\alpha
. Тогда
\angle B_{1}MC_{1}=\angle PMQ-(\angle QMB_{1}+\angle PMC_{1})=
=\alpha-(\angle QMB_{1}+\angle MB_{1}Q)=\alpha-(180^{\circ}-\angle MQB_{1})=
=\alpha-180^{\circ}+\angle MQB_{1}=\alpha-180^{\circ}+(180^{\circ}-\alpha+2\varphi)=2\varphi.
(Случай, когда \angle C_{1}PB+\angle BPM\gt180^{\circ}
, разбирается аналогично.)
Лемма доказана.
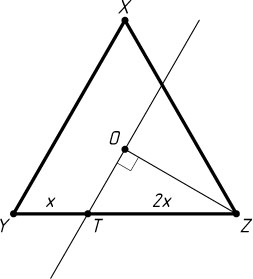
Возвратимся к нашей задаче. Заметим, что если через точку T
, лежащую на стороне YZ
равностороннего треугольника XYZ
с центром O
и делящую это сторону в отношении YT:TZ=1:2
, провести прямую, параллельную стороне XY
(рис. 5), то эта прямая пройдёт через точку O
и \angle ZOT=90^{\circ}
.
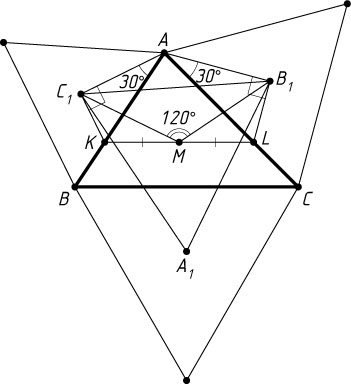
Отметим на сторонах AB
и AC
данного треугольника ABC
такие точки K
и L
, что BK:AK=1:2
и CL:AL=1:2
(рис. 6). Тогда KL\parallel BC
, а середина M
отрезка KL
— точка пересечения медиан треугольника ABC
. Построим внешним образом на сторонах AK
и AL
треугольника AKL
как на гипотенузах прямоугольные треугольники AC_{1}K
и AB_{1}L
с углами 60^{\circ}
при вершинах K
и L
. Тогда точки C_{1}
и B_{1}
— центры правильных треугольников, о которых говорится в условии задачи. По доказанной лемме, MC_{1}=MB_{1}
и \angle B_{1}MC_{1}=2\angle ALB_{1}=120^{\circ}
.
Если A_{1}
— центр равностороннего треугольника, построенного внешним образом на стороне BC
, то аналогично докажем, что MA_{1}=MB_{1}
и \angle A_{1}MB_{1}=120^{\circ}
. Следовательно, A_{1}B_{1}C_{1}
— равносторонний треугольник, а M
— его центр.
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 92, с. 30
Источник: Яглом И. М. Геометрические преобразования. — Т. 1: Движения и преобразования подобия. — М.: ГИТТЛ, 1955. — № 20(a), с. 40
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 57, с. 186
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 18.38(a), с. 72
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 1.49(б), с. 15
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 18.42(а), с. 377
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 78
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 42, с. 9
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 11.5, с. 87




