6053. Около окружности описана прямоугольная трапеция. Через вершину её острого угла проведите прямую, делящую трапецию на две равновеликие части.
Ответ. Искомая прямая проходит через центр окружности.
Решение. Первый способ. Пусть окружность радиуса r
с центром O
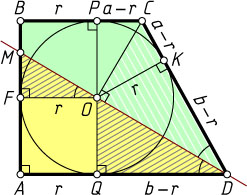
, вписанная в прямоугольную трапецию с основаниями BC=a
и AD=b
(a\lt b
), касается большей боковой стороны CD
в точке K
, меньшей боковой стороны AB
— в точке F
, а оснований BC
и AD
— в точках P
и Q
соответственно.
Тогда
CK=CP=BC-BP=a-r,~DK=DQ=AD-AQ=b-r.
Отрезок OK
— высота прямоугольного треугольника COD
, проведённая из вершины прямого угла (см. задачу 313), поэтому OK^{2}=CK\cdot DK
, или r^{2}=(a-r)(b-r)
. Отсюда находим, что r=\frac{ab}{a+b}
. Следовательно,
S_{ABCD}=\frac{BC+AD}{2}\cdot AB=\frac{a+b}{2}\cdot2r=\frac{a+b}{2}\cdot2\cdot\frac{ab}{a+b}=ab.
Пусть луч DO
(биссектриса острого угла трапеции) пересекает сторону AB
в точке M
. Прямоугольные треугольники OFM
и DQO
подобны, поэтому \frac{MF}{OQ}=\frac{OF}{DQ}
, откуда
MF=\frac{OQ\cdot OF}{DQ}=\frac{r^{2}}{b-r}.
Тогда
AM=AF+MF=r+\frac{r^{2}}{b-r}=\frac{br}{b-r}=\frac{b\cdot\frac{ab}{a+b}}{b-\frac{ab}{a+b}}=a,
S_{\triangle AMD}=\frac{1}{2}AD\cdot AM=\frac{1}{2}b\cdot a=\frac{ab}{2}.
Следовательно, прямая DO
разбивает трапецию ABCD
на две равновеликие части.
Второй способ. Заметим, что равны прямоугольные треугольники OKC
, OPC
и OFM
(обозначим их площади через s_{1}
), а также — прямоугольные треугольники DKO
и DQO
(обозначим их площади через s_{2}
). Площади равных квадратов AMOQ
и BMOP
обозначим через s_{3}
. Тогда
S_{\triangle AMD}=s_{1}+s_{2}+s_{3},
S_{ABCD}=S_{\triangle DKO}+S_{\triangle DQO}+S_{\triangle OKC}+S_{\triangle OPC}+S_{AMOQ}+S_{BMOP}=
=2s_{1}+2s_{2}+2s_{3}=2(s_{1}+s_{2}+s_{3})=2S_{\triangle AMD}.
Следовательно, прямая DO
разбивает трапецию ABCD
на две равновеликие части.
Примечание. (К первому способу.) Равенство AM=BC=a
можно доказать по-другому: см. задачу 1019.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 738, с. 93
