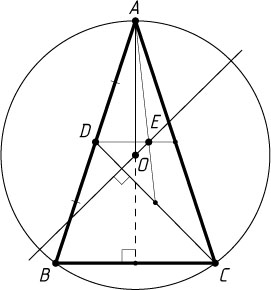
6246. Пусть O
— центр окружности, описанной около равнобедренного треугольника ABC
(AB=AC
), D
— середина стороны AB
, а E
— точка пересечения медиан треугольника ACD
. Докажите, что OE\perp CD
.
Указание. Докажите, что \overrightarrow{OE}\cdot\overrightarrow{CD}=0
.
Решение. Первый способ. Поскольку D
— середина отрезка AB
,
\overrightarrow{OD}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})
(см. задачу 4500), поэтому (см. задачу 4505)
\overrightarrow{OE}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OD})=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OC}+\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB}))=
=\frac{1}{6}(3\overrightarrow{OA}+2\overrightarrow{OC}+\overrightarrow{OB}).
Кроме того
\overrightarrow{CD}=\frac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB})=\frac{1}{2}((\overrightarrow{CO}+\overrightarrow{OA})+(\overrightarrow{CO}+\overrightarrow{OB}))=
=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB}-2\overrightarrow{OC}).
Значит,
12\overrightarrow{OE}\cdot\overrightarrow{CD}=(3\overrightarrow{OA}+2\overrightarrow{OC}+\overrightarrow{OB})(\overrightarrow{OA}+\overrightarrow{OB}-2\overrightarrow{OC})=
=3\overrightarrow{OA}^{2}+3\overrightarrow{OA}\cdot\overrightarrow{OB}-6\overrightarrow{OA}\cdot\overrightarrow{OC}+2\overrightarrow{OC}\cdot\overrightarrow{OA}+2\overrightarrow{OC}\cdot\overrightarrow{OB}-4\overrightarrow{OC}^{2}+
+\overrightarrow{OA}\cdot\overrightarrow{OB}+\overrightarrow{OB}^{2}-2\overrightarrow{OB}\cdot\overrightarrow{OC}=
=3R^{2}-4R^{2}+R^{2}+4\overrightarrow{OA}\cdot\overrightarrow{OB}-4\overrightarrow{OA}\cdot\overrightarrow{OC}=
=4\overrightarrow{OA}(\overrightarrow{OB}-\overrightarrow{OC})=4\overrightarrow{OA}\cdot\overrightarrow{CB}=0,
так как OA\perp BC
(R
— радиус окружности). Следовательно, OE\perp CD
.
Второй способ. Пусть медиана (она же высота) AH
и медиана CD
треугольника ABC
пересекаются в точке G
, а F
— середина боковой стороны AC
. Тогда точка E
лежит на медиане DF
треугольника ADC
, и DE=\frac{2}{3}DF
.
Поскольку AD\perp OD
и AG\perp DE
, то достаточно доказать, что треугольники ADG
и DOE
подобны. Отсюда будет следовать, что их третьи стороны DG
и OE
тоже перпендикулярны.
Отметим на отрезке CH
такую точку I
, что HI=\frac{1}{3}CH
. Поскольку \frac{HG}{HA}=\frac{1}{3}=\frac{HI}{HC}
, то GI\parallel AC
, поэтому
\angle IGH=\angle CAH=\angle DAG=\angle DAO=\angle EDO.
Таким образом, осталось доказать, что \frac{AG}{AD}=\frac{DE}{DO}
.
Отрезок DF
— средняя линия треугольника ABC
, поэтому
DF=\frac{1}{2}BC=CH=3IH,
Значит,
DE=\frac{2}{3}DF=\frac{2}{3}\cdot3IH=2IH.
Острые углы при вершинах G
и A
прямоугольных треугольников GHI
и ADO
равны, значит, эти треугольники подобны. Тогда \frac{GH}{AD}=\frac{HI}{DO}
, поэтому
\frac{AG}{AD}=\frac{2GH}{AD}=\frac{2HI}{DO}=\frac{DE}{DO}.
Отсюда следует утверждение задачи.
Источник: Зарубежные математические олимпиады. — 1983, Англия
Источник: Конягин С. В. и др. Зарубежные математические олимпиады / Под ред. И. Н. Сергеева. — М.: Наука, 1987. — № 9.10, с. 32, Англия, 1983 г.
Источник: Журнал «Crux Mathematicorum». — 1991, № 4, задача 1, с. 105
Источник: Британская математическая олимпиада. — 1983
