6434. Теорема о центрах трёх гомотетий. Общие внешние касательные к окружностям S_{1}
и S_{2}
, S_{2}
и S_{3}
, S_{1}
и S_{3}
пересекаются в точках A
, B
и C
соответственно. Докажите, что точки A
, B
и C
лежат на одной прямой.
Указание. Примените либо теорему о композиции гомотетий (см. задачу 6433), либо теорему Менелая (см. задачу 1622) к треугольнику с вершинами в центрах окружностей.
Решение. Первый способ. Точка A
— центр гомотетии, переводящей окружность S_{1}
в S_{2}
(рис. 1), B
— центр гомотетии, переводящей окружность S_{2}
в S_{3}
, а точка C
— центр гомотетии, переводящей окружность S_{3}
в S_{1}
, причём коэффициенты этих гомотетий положительны, так как рассматриваются внешние общие касательные. Композиция первых двух гомотетий есть гомотетия с положительным коэффициентом, центр C
которой лежит на прямой, проходящей через центры A
и B
первых двух (см. задачу 6433).
Второй способ. Рассмотрим случай, изображённый на рис. 2. Пусть O_{1}
, O_{2}
, O_{3}
— центры окружностей S_{1}
, S_{2}
, S_{3}
; r_{1}
, r_{2}
, r_{3}
— их радиусы.
Если A
— точка пересечения общих внешних касательных окружностей S_{1}
и S_{2}
, то гомотетия с центром A
и коэффициентом \frac{r_{2}}{r_{1}}
переводит окружность S_{1}
в окружность S_{2}
.
Если B
— точка пересечения общих внешних касательных окружностей S_{2}
и S_{3}
, то гомотетия с центром B
и коэффициентом \frac{r_{2}}{r_{3}}
переводит окружность S_{3}
в окружность S_{2}
.
Если C
— точка пересечения общих внешних касательных окружностей S_{1}
и S_{3}
, то гомотетия с центром C
и коэффициентом \frac{r_{1}}{r_{3}}
переводит окружность S_{3}
в окружность S_{1}
. Тогда
\frac{O_{1}A}{AO_{2}}\cdot\frac{O_{2}B}{BO_{3}}\cdot\frac{O_{3}C}{CO_{1}}=\frac{r_{1}}{r_{2}}\cdot\frac{r_{2}}{r_{3}}\cdot\frac{r_{3}}{r_{1}}=1.
Следовательно, по теореме Менелая (см. задачу 1622) точки A
, B
и C
лежат на одной прямой. Аналогично для любого другого случая.
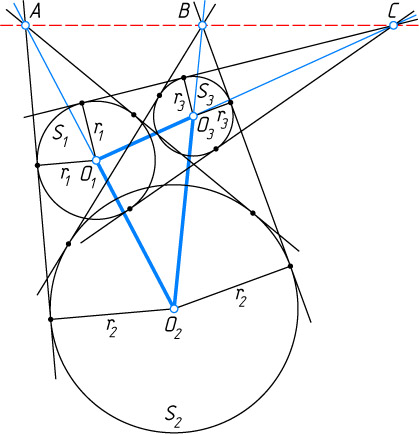
Примечание. Верно следующее общее утверждение. Если композиция трёх гомотетий является тождественным преобразованием, то их центры лежат на одной прямой.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 19.24, с. 87
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 19.34, с. 391