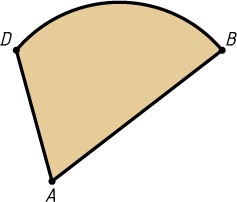
6503. Плоская выпуклая фигура ограничена отрезками AB
и AD
и дугой BD
некоторой окружности (см.рис.). Постройте какую-нибудь прямую, которая делит пополам: а) периметр этой фигуры; б) её площадь.
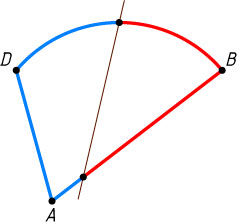
Решение. а) Достаточно провести прямую через середину дуги и середину ломаной BAD
.
б) Пусть A
— вершина угла BAD
, B
и D
— концы дуги, C
— её середина. Сегменты, опирающиеся на хорды BC
и CD
равны. Поэтому достаточно провести через точку C
прямую, которая делит пополам площадь четырёхугольника ABCD
.
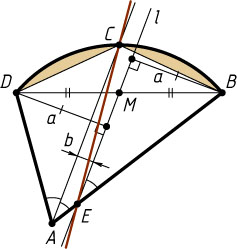
Проведём через середину M
диагонали BD
прямую l
, параллельную AC
. Пусть она пересекает сторону AB
в точке E
(случай пересечения прямой l
со стороной AD
рассматривается аналогично). Докажем, что прямая CE
делит пополам площадь четырёхугольника ABCD
.
Действительно, S_{AMCD}=\frac{1}{2}S_{ABCD}
, так как CM
и AM
— медианы треугольников BCD
и ABD
, а медиана треугольника разбивает его на два равновеликих треугольника (см. задачу 3001). Пусть O
— точка пересечения диагоналей трапеции AEMC
. Тогда треугольники COM
и AOE
равновелики (см. задачу 3017). Следовательно,
S_{ADCE}=S_{AMCD}=\frac{1}{2}S_{ABCD}.
Что и требовалось доказать.
Автор: Произволов В. В.
Автор: Сендеров В. А.
Источник: Московская математическая олимпиада. — 1999, LXII, 11 класс
Источник: Журнал «Квант». — 1999, № 4, с. 50
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 2, с. 43


