6538. В остроугольном треугольнике ABC
на высоте BK
как на диаметре построена окружность S
, пересекающая стороны AB
и BC
в точках E
и F
соответственно. К окружности S
в точках E
и F
проведены касательные. Докажите, что их точка пересечения лежит на прямой, содержащей медиану треугольника ABC
, проведённую из вершины B
.
Указание. Рассмотрите гомотетию с центром в точке B
(или см. задачи 10449 и 10341).
Решение. Первый способ. При гомотетии с центром в точке B
окружность S
переходит в окружность S'
, касающуюся окружности S
в точке B
. Если при этом точка A
переходит в точку A'
, а точка C
— в C
, то точки A'
и C'
лежат на прямых BA
и BC
соответственно, касательная AC
к окружности S
переходит в касательную A'C'
к окружности S'
, медиана BN
треугольника ABC
— в медиану BN'
треугольника A'BC'
. Если мы докажем, что касательные к окружности S'
, проведённые в точках E'
и F'
, соответствующих точкам E
и F
, пересекаются на медиане BN'
треугольника A'BC'
, то, рассмотрев обратную гомотетию, получим утверждение исходной задачи.
Пусть H
— точка пересечения высот треугольника ABC
. В качестве окружности S'
возьмём окружность с диаметром BH
и докажем, что прямая E'N
касается окружности S'
.
Действительно, поскольку HE'\perp AB
, то CE'
— высота треугольника ABC
. Тогда \angle ABK=\angle ACE'
, а так как E'N
— медиана прямоугольного треугольника AE'C
, проведённая из вершины прямого угла, то (см. задачу 1109)
\angle NE'C=\angle NCE'=\angle ACE'=\angle ABK=\angle E'BH.
Тогда, если O
— центр окружности S'
, то
\angle OE'N=\angle OE'H+\angle NE'C=(90^{\circ}-\angle OE'B)+\angle E'BH=(90^{\circ}-\angle E'BH)+\angle E'BH=90^{\circ}.
следовательно, NE'
— касательная к окружности S'
. Аналогично докажем, что NF'
— также касательная к S'
.
Таким образом, касательные, проведённые к окружности S'
в точках E'
и F'
пересекаются на прямой, содержащей медиану треугольника ABC
, проведённую из вершины B
. Следовательно, касательные к гомотетичной S'
окружности S
, проведённые в соответствующих точках E
и F
, также пересекаются на этой прямой.
Второй способ. Прямая BP
содержит симедиану треугольника BEF
(см. задачу 10449), а так как
\angle BFE=\angle BKE=\angle BAC,
то отрезки EF
и AC
антипараллельны. Следовательно, прямая BP
содержит медиану треугольника ABC
(см. задачу 10341а).
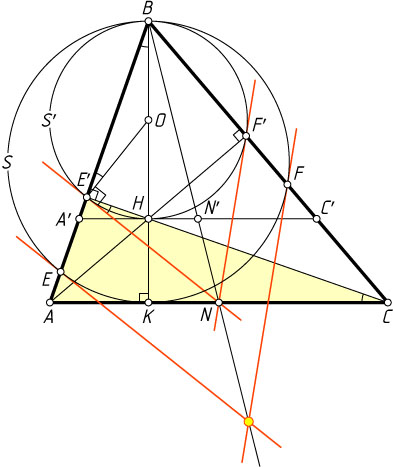
Примечание. См. также статью Ю.Блинкова «Симедиана», Квант, 2015, N4, с.35-39.