6648. В треугольнике ABC
высота и медиана из вершины A
образуют (вместе с прямой BC
) треугольник, в котором биссектриса угла A
является медианой, а высота и медиана из вершины B
образуют (вместе с прямой AC
) треугольник, в котором биссектриса угла B
является биссектрисой. Найдите отношение сторон треугольника ABC
.
Ответ. 1:2\sqrt{2}:3
.
Решение. Пусть AM
— медиана, а AL
— биссектриса треугольника ABC
. Поскольку биссектриса угла B
делит пополам угол между высотой и медианой, проведёнными из вершины B
, угол B
— прямой (см. задачу 84). Значит, высота, проведённая из вершины A
совпадает со стороной AB
.
Положим
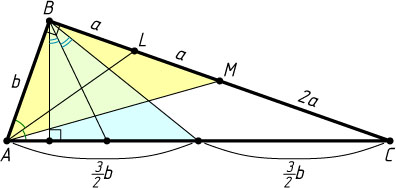
BL=LM=a,~CM=2a,~AB=b.
Тогда LC=3a
, а так как биссектриса AL
треугольника BAC
является медианой треугольника BAM
, то (см. задачу 1509)
\frac{AB}{AC}=\frac{BL}{LC}=\frac{a}{3a}=\frac{1}{3},~AC=3AB=3b.
По теореме Пифагора BC^{2}+AB^{2}=AC^{2}
, или b^{2}+16a^{2}=9b^{2}
, откуда b=a\sqrt{2}
. Тогда
AB=a\sqrt{2},~BC=4a,~AC=3a\sqrt{2}.
Следовательно, AB:BC:AC=1:2\sqrt{2}:3
.
