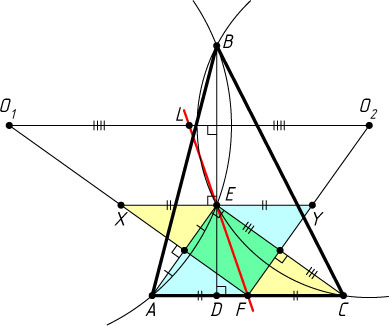
6674. На высоте BD
треугольника ABC
взята такая точка E
, что \angle AEC=90^{\circ}
. Точки O_{1}
и O_{2}
— центры описанных окружностей треугольников AEB
и CEB
соответственно, F
и L
— середины отрезков соответственно AC
и O_{1}O_{2}
. Докажите, что точки L
, E
и F
лежат на одной прямой.
Решение. Серединный перпендикуляр к отрезку AE
и прямая EC
параллельны, так как они обе перпендикулярны прямой AE
. Аналогично серединный перпендикуляр к отрезку CE
параллелен AE
. По теореме Фалеса эти серединные проходят через середину AC
, т. е. через точку F
.
Пусть прямая, проходящая через E
параллельно AC
, пересекает FO_{1}
и FO_{2}
в точках X
и Y
соответственно. Поскольку FCEX
и FAEY
— параллелограммы,
XE=FC=FA=EY,
т. е. FE
— медиана треугольника XFY
, а так как O_{1}O_{2}\perp BD
(см. задачу 1130) и AC\perp BD
, то O_{1}O_{2}\parallel AC\parallel XY
. Следовательно, прямая FE
проходит через середину L
отрезка O_{1}O_{2}
(см. задачу 2607).
