6675. На стороне BC
равностороннего треугольника ABC
взяты точки M
и N
(M
лежит между B
и N
) такие, что \angle MAN=30^{\circ}
. Описанные окружности треугольников AMC
и ANB
пересекаются в точке K
. Докажите, что прямая AK
содержит центр описанной окружности треугольника AMN
.
Решение. Композиция симметрий относительно пересекающихся прямых AM
и AN
есть поворот вокруг точки A
их пересечения на угол, вдвое больший угла между этими прямыми (см. задачу 5107), т. е. на угол 60^{\circ}
. Значит, точка, симметричная B
относительно AM
, совпадает с точкой, симметричной C
относительно AN
. Обозначим эту точку через L
. Тогда
60^{\circ}=\angle ACM=\angle ABM=\angle ALM,
т. е. L
лежит на описанной окружности треугольника ACM
. Аналогично L
лежит на описанной окружности треугольника ABN
и, значит, совпадает с K
.
Из симметрии \angle KAN=\angle NAC
, а так как AMN
— внешний угол треугольника ABM
, то
\angle KAN=\angle NAC=30^{\circ}-\angle BAM=
=30^{\circ}-(\angle AMN-\angle ABM)=30^{\circ}-(\angle AMN-60^{\circ})=
=90^{\circ}-\angle NMA=\angle HAM,
где AH
— высота треугольника MAN
.
Пусть O
— центр описанной окружности треугольника AMN
. Тогда \angle OAN=\angle HAM
(см. задачу 20), а так как \angle KAN=\angle OAN=\angle HAM
, то точка O
лежит на прямой AK
. Что и требовалось доказать.
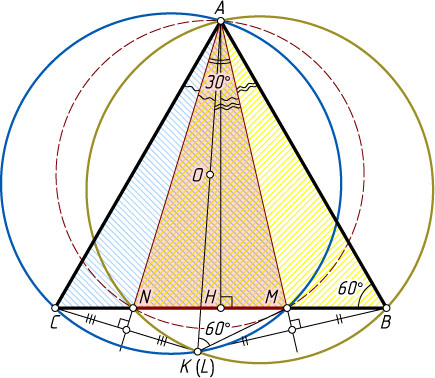
Автор: Швецов Д. В.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2010, VI, заочный тур, № 6, 8-9 классы
