6682. В угол с вершиной A
вписана окружность, касающаяся сторон угла в точках B
и C
. Прямая, проходящая через точку A
, пересекает окружность в точках D
и E
. Хорда BX
параллельна прямой DE
. Докажите, что отрезок XC
проходит через середину отрезка DE
.
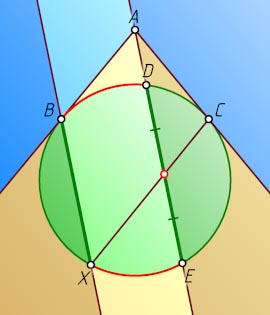
Решение. Первый способ. Прежде всего заметим, что \angle BCD=\angle ECX
, так как соответствующие дуги заключены между параллельными хордами (рис. 1). Кроме того, из равенства углов ABD
и AEB
следует подобие треугольников ABD
и AEB
и, значит, равенство \frac{BD}{BE}=\frac{AD}{AB}
. Аналогично получаем, что \frac{CD}{CE}=\frac{AD}{AC}=\frac{AD}{AB}
, т. е.
BD\cdot CE=CD\cdot BE=\frac{1}{2}BC\cdot DE
(последнее равенство следует из теоремы Птолемея, см. задачу 130).
Пусть теперь CX
пересекает DE
в точке M
. Тогда треугольники CBD
и CEM
подобны, значит, \frac{BD}{ME}=\frac{BC}{CE}
, или BD\cdot CE=BC\cdot ME
. Значит,
BC\cdot ME=BD\cdot CE=\frac{1}{2}BC\cdot DE,
откуда ME=\frac{1}{2}DE
. Следовательно, M
— середина DE
.
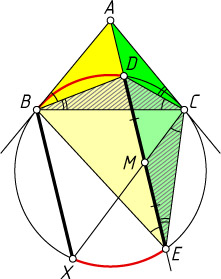
Второй способ. (Александр Руденко, лицей №171 «Лидер», Киев.) Заметим (рис. 2), что
\angle DMC=\frac{1}{2}(\smile DC+\smile XE)
(см. задачу 26). По условию DE\parallel BX
, поэтому \smile BD=\smile EX
. С другой стороны, если O
— центр окружности, то
\angle COB=\smile CB=\smile CD+\smile DB=\smile CD+\smile EX=2\angle CMD,
откуда следует, что
\angle COA=\frac{1}{2}\angle COB=\angle CMD,
поэтому точки A
, C
, M
, O
лежат на одной окружности, а так как \angle ACO=90^{\circ}
, то OA
— диаметр этой окружности. Значит, \angle AMO=\angle ACO=90^{\circ}
, т. е. OM\perp DE
. Следовательно, DM=ME
.
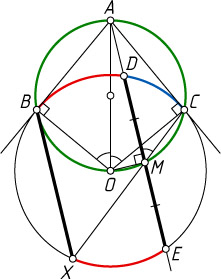
Автор: Нилов Ф. К.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2010, VI, заочный тур, № 16, 9-11 классы


