6694. В прямоугольном треугольнике ABC
(\angle B=90^{\circ}
) проведена высота BH
. Окружность, вписанная в треугольник ABH
, касается сторон AB
и AH
в точках H_{1}
и B_{1}
соответственно; окружность, вписанная в треугольник CBH
, касается сторон CB
и CH
в точках H_{2}
и B_{2}
соответственно. Пусть O
— центр описанной окружности треугольника H_{1}BH_{2}
. Докажите, что OB_{1}=OB_{2}
.
Решение. Обозначим \angle ACB=\alpha
. Пусть I_{1}
и I_{2}
— центры вписанных окружностей треугольников ABH
и CBH
соответственно. Из подобия этих треугольников следует, что
\frac{I_{1}H_{1}}{I_{2}H_{2}}=\frac{AB}{BC}=\tg\alpha
(см. задачу 2602).
Поскольку отрезки I_{1}H_{1}
и I_{2}H_{2}
перпендикулярны соответственно AB
и BC
, проекции этих отрезков на AC
равны I_{1}H_{1}\cos\alpha
и I_{2}H_{2}\sin\alpha
, а так как
\frac{I_{1}H_{1}\cos\alpha}{I_{2}H_{2}\sin\alpha}=\frac{I_{1}H_{1}}{I_{2}H_{2}}\cdot\frac{\cos\alpha}{\sin\alpha}=\tg\alpha\ctg\alpha=1,
то эти проекции равны. Тогда, так как O
— середина H_{1}H_{2}
, то проекция M
точки O
на AC
совпадает с серединой проекции отрезка H_{1}H_{2}
на AC
(см. задачу 1939). Значит, M
— середина B_{1}B_{2}
, а OM
— высота и медиана треугольника B_{1}OB_{2}
. Следовательно, OB_{1}=OB_{2}
.
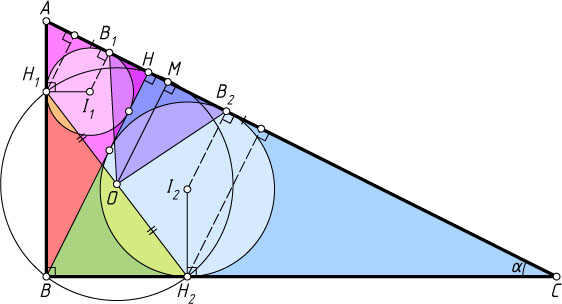
Автор: Швецов Д. В.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2010, VI, финальный тур, № 5, 10 класс
