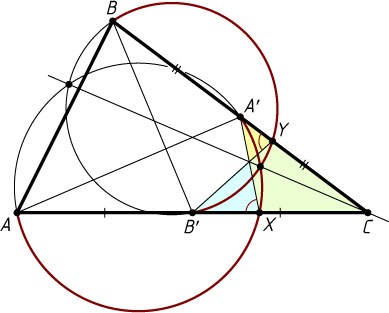
6751. На медианах AA'
и BB'
треугольника ABC
построены в сторону вершины C
дуги с одинаковой градусной мерой. Докажите, что общая хорда окружностей, содержащих эти дуги, проходит через точку C
.
Решение. Пусть окружность, построенная на AA'
, пересекает AC
в точке X
, а окружность, построенная на BB'
, пересекает BC
в точке Y
. Поскольку \angle AXA'=\angle BYB'
, треугольники CXA'
и CYB'
подобны, значит, \frac{CX}{CA'}=\frac{CY}{CB'}
, или CX\cdot CB'=CY\cdot CA'
. Тогда
CX\cdot CA=2CX\cdot CB'=2CY\cdot CA'=CY\cdot CB.
Значит, степени точки C
относительно обеих окружностей равны, следовательно, она лежит на их радикальной оси (см. задачу 6391), т. е. на прямой, содержащей общую хорду окружностей (см. задачу 6392).
Автор: Ясинский В. А.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2008, IV, финальный тур, № 7, 10 класс
