6809. Остроугольный треугольник ABC
(AB\lt AC)
вписан в окружность \Omega
. Пусть M
— точка пересечения его медиан, а AH
— высота этого треугольника. Луч MH
пересекает \Omega
в точке A'
. Докажите, что окружность, описанная около треугольника A'HB
, касается AB
.
Решение. Первый способ. Пусть D
— точка, симметричная вершине A
относительно серединного перпендикуляра к хорде BC
, т. е. относительно диаметра окружности \Omega
. Тогда точка D
лежит на \Omega
(см. задачу 1677). При этом проекция H'
точки D
на BC
симметрична точке H
, и точки H
и H'
симметричны относительно середины K
стороны BC
.
Пусть X
— точка пересечения DH
и AK
. Треугольник AXD
подобен треугольнику KXH
, поэтому
\frac{AX}{XK}=\frac{AD}{KH}=\frac{HH'}{KH}=2.
Значит, точка X
совпадает с точкой M
пересечения медиан треугольника ABC
. Из симметрии и теоремы о вписанных углах
\angle ABH=\angle ABC=\angle DCB=\angle DA'B=\angle HA'B.
Следовательно, AB
— касательная к окружности, описанной около треугольника A'HB
(см. задачу 144).
Второй способ. Точка H
лежит на окружности \omega
, проходящей через середины сторон треугольника ABC
(см. задачу 174). При гомотетии с центром M
и коэффициентом -2
эта окружность переходит в окружность \Omega
, описанную около треугольника ABC
. Значит, точка H
при этой гомотетии переходит в такую точку D
окружности \Omega
, что DA\parallel BC
. Поэтому точки H
, M
и D
лежат на одной прямой. Далее см. первый способ.
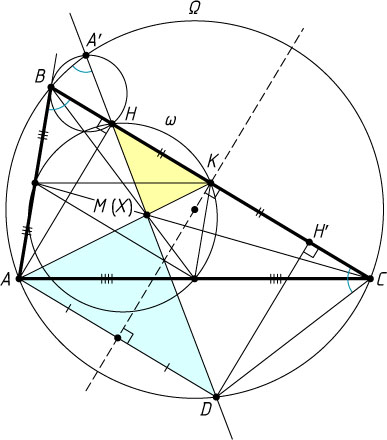
Автор: Гольдшейд И.
Автор: Якубов А. Г.
Источник: Всероссийская олимпиада школьников. — 2014-2015, XLI, заключительный этап, 9 класс
