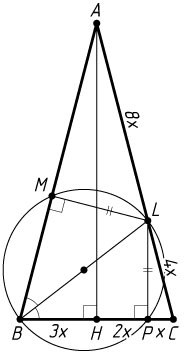
6866. Окружность, построенная на биссектрисе BL
равнобедренного треугольника ABC
как на диаметре, пересекает основание BC
в точке P
. Боковая сторона треугольника вдвое больше его основания.
а) Докажите, что отрезок BP
в пять раз больше отрезка CP
.
б) Пусть указанная окружность пересекает сторону AB
в точке M
. Найдите BL
, если ML=\frac{\sqrt{15}}{2}
.
Ответ. \sqrt{10}
.
Решение. а) Пусть AH
— высота треугольника ABC
. Точка P
лежит на окружности с диаметром BL
, поэтому \angle BPL=90^{\circ}
, значит, LP\parallel AH
. По теореме о пропорциональных отрезках и свойству биссектрисы треугольника (см. задачу 1509)
\frac{CP}{PH}=\frac{CL}{LA}=\frac{BC}{AB}=\frac{1}{2}.
Значит,
PC=\frac{1}{3}CH=\frac{1}{3}\cdot\frac{1}{2}BC=\frac{1}{6}BC.
Следовательно, BP=5CP
.
б) Пусть BC=6x
, AB=AC=12x
. Тогда
CP=\frac{1}{6}BC=x,~CL=\frac{1}{3}AC=4x.
Точка L
лежит на биссектрисе угла ABC
, поэтому она равноудалена от сторон этого угла (см. задачу 1138), а так как \angle BML=\angle BPL=90^{\circ}
, то LP=LM=\frac{\sqrt{15}}{2}
. По теореме Пифагора CL^{2}=LP^{2}+CP^{2}
, или 16x^{2}=\frac{15}{4}+x^{2}
. Отсюда находим, что x=\frac{1}{2}
. Тогда PB=5x=\frac{5}{2}
. Следовательно,
BL=\sqrt{BP^{2}+LP^{2}}=\sqrt{\frac{25}{4}+\frac{15}{4}}=\sqrt{10}.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2015
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5.30.1, с. 51; № 11.49.2, с. 119
