6875. Трапеция ABCD
вписана в окружность радиуса R
и описана около окружности радиуса r
, причём R=2r
. Найдите среднюю линию трапеции, если диагональ AC
равна 4
.
Ответ. \sqrt{17}-1
.
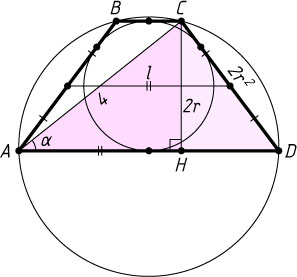
Решение. Обозначим \angle CAD=\alpha
. Пусть CH
— высота трапеции. Тогда
CH=2r,~\sin\alpha=\frac{CH}{AC}=\frac{2r}{4}=\frac{r}{2}.
Окружность, описанная около трапеции, — это окружность, описанная около треугольника ACD
. По теореме синусов
CD=2R\sin\alpha=4r\cdot\frac{r}{2}=2r^{2},
Пусть средняя линия трапеции равна l
. Трапеция ABCD
равнобедренная и описанная, поэтому l=AH=CD=2r^{2}
(см. задачи 1021 и 1930). По теореме Пифагора
AH^{2}+CH^{2}=AC^{2},~\mbox{или}~4r^{4}+4r^{2}=16,
откуда находим, что r^{2}=\frac{\sqrt{17}-1}{2}
. Следовательно,
l=2r^{2}=\sqrt{17}-1.
Источник: Дополнительное вступительное испытание в МГУ. — 2013, июль, вариант 2, № 6
