7279. В треугольной пирамиде ABCD
известно, что CD=a
, а перпендикуляр, опущенный из середины ребра AB
на CD
, равен b
и образует равные углы \alpha
с гранями ACD
и BCD
. Найдите объём пирамиды.
Ответ. \frac{1}{3}ab^{2}\tg\alpha
.
Указание. Достройте тетраэдр ABCD
до треугольной призмы ABCEFD
и рассмотрите перпендикулярное сечение этой призмы (или примените формулу из задачи 9415).
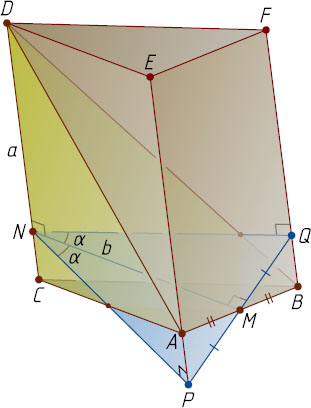
Решение. Первый способ. Пусть M
— середина ребра AB
, а точка N
лежит на ребре CD
, причём MN\perp CD
и MN=b
. Достроим тетраэдр ABCD
до треугольной призмы ABCEFD
(AE\parallel BF\parallel CD
) и проведём через прямую MN
плоскость, перпендикулярную ребру CD
. Пусть эта плоскость пересекает прямые AE
и BF
соответственно в точках P
и Q
. Тогда треугольник NPQ
— перпендикулярное сечение призмы, а \angle MNQ=\angle MNP=\alpha
. Из равенства треугольников AMP
и BMQ
следует, что M
— середина PQ
, поэтому биссектриса NM
треугольника NPQ
является его медианой, значит, треугольник NPQ
— равнобедренный. Поскольку MP=MN\tg\alpha=b\tg\alpha
,
S_{\triangle NPQ}=\frac{1}{2}PQ\cdot MN=MP\cdot MN=b^{2}\tg\alpha.
Объём призмы равен произведению площади её перпендикулярного сечения на боковое ребро (см. задачу 7310), поэтому
V_{ABCEFD}=S_{\triangle NPQ}\cdot CD=ab^{2}\tg\alpha.
Следовательно,
V_{ABCD}=\frac{1}{3}V_{ABCEFD}=\frac{1}{3}ab^{2}\tg\alpha.
Второй способ. Объём пирамиды ABCD
равен третьей части произведения её бокового ребра CD
на площадь S'
ортогональной проекции основания пирамиды на плоскость, перпендикулярную ребру CD
(см. задачу 9415). Поскольку S'=b^{2}\tg\alpha
, то
V=\frac{1}{3}CD\cdot S'=\frac{1}{3}a\cdot b^{2}\tg\alpha=\frac{1}{3}ab^{2}\tg\alpha.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1973, вариант 2, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 268
