7297. Докажите, что правильную треугольную пирамиду можно пересечь плоскостью так, чтобы в сечении получился квадрат. Найдите сторону этого квадрата, если сторона основания равна a
, а боковое ребро равно b
.
Ответ. \frac{ab}{a+b}
.
Указание. Рассмотрите сечение пирамиды плоскостью, параллельной двум противоположным рёбрам.
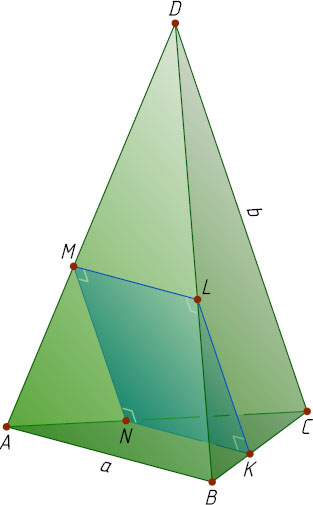
Решение. Через точку M
ребра DA
проведём плоскость, параллельную рёбрам AB
и CD
правильной треугольной пирамиды ABCD
с вершиной D
. Пусть эта плоскость пересекает рёбра BC
, BD
и AC
в точках K
, L
и N
соответственно.
Через прямую AB
проходит плоскость ABD
, пересекающая секущую плоскость по прямой ML
, значит, ML\parallel AB
(см. задачу 8003). Аналогично CK\parallel CD
, KN\parallel AB
и MN\parallel CD
. Противоположные стороны четырёхугольника KLMN
попарно параллельны, значит, это параллелограмм, а так как противоположные рёбра правильной треугольной пирамиды попарно перпендикулярны (см. задачу 7000), это прямоугольник.
Докажем, что точку M
можно выбрать так, чтобы стороны этого параллелограмма были равны. Пусть AB=a
и CD=b
. Отметим на ребре AD
такую точку M
, чтобы \frac{AM}{AD}=\frac{a}{a+b}
. Тогда
\frac{MN}{CD}=\frac{AM}{AD}=\frac{a}{a+b},~MN=CD\cdot\frac{a}{a+b}=\frac{ab}{a+b},
\frac{ML}{AB}=\frac{DM}{AD}=\frac{AD-AM}{AD}=1-\frac{AM}{AD}=1-\frac{a}{a+b}=\frac{b}{a+b},
Значит,
ML=AB\cdot\frac{b}{a+b}=\frac{ab}{a+b}=MN.
Следовательно, при таком выборе точки M
четырёхугольник KLMN
— квадрат.
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 16, с. 8
