9569. На рёбрах AB
и BC
треугольной пирамиды DABC
отмечены точки M
и N
так, что AM:MB=CN:NB=1:2
. Точки P
и Q
— середины рёбер DA
и DC
соответственно.
а) Докажите, что точки P
, Q
, M
и N
лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость PQM
разбивает пирамиду.
Ответ. 13:23
.
Решение. Первый способ. а) Поскольку AM:MB=CN:NB
, прямая MN
параллельна ребру AC
, а так как PQ
— средняя линия треугольника ADC
, то PQ\parallel AC
. Значит, прямые MN
и PQ
параллельны, поэтому они лежат в одной плоскости. Следовательно, принадлежащие им точки P
, Q
, M
и N
лежат в этой плоскости.
б) Пусть объём пирамиды равен V
, площадь грани ABC
равна S
, а высота пирамиды, опущенная из вершины D
, равна h
. Тогда V=\frac{1}{3}Sh
.
Пусть K
— середина ребра AC
, а L
и T
— точки пересечения прямой, проходящей через точку K
параллельно AB
, с отрезком MN
и стороной BC
. Тогда T
— середина ребра BC
, APQK
и AKLM
— параллелограммы, а объём содержащей точку A
части пирамиды, равен сумме объёмов треугольной призмы AMPKLQ
и четырёхугольной пирамиды QCKLN
с вершиной Q
. Обозначим эти объёмы v
, v_{1}
и v_{2}
соответственно.
Далее получаем, что
S_{\triangle BMN}=\left(\frac{2}{3}\right)^{2}S=\frac{4}{9}S,~S_{AMNC}=S-\frac{4}{9}S=\frac{5}{9}S,
S_{\triangle CKT}=\frac{1}{4}S,~S_{CKLN}=S_{\triangle CKT}-S_{\triangle NLT}=S_{\triangle CKT}-\frac{1}{9}S_{\triangle CKT}=\frac{1}{4}S-\frac{1}{9}\cdot\frac{1}{4}S=\frac{2}{9}S,
v_{2}=\frac{2}{9}\cdot\frac{1}{2}V=\frac{1}{9}V,
S_{AMLK}=S_{AMNC}-S_{CKLN}=\frac{5}{9}S-\frac{2}{9}S=\frac{1}{3}S,
v_{1}=\frac{1}{2}S_{AMLK}\cdot\frac{1}{2}h=\frac{1}{2}\cdot\frac{1}{3}S\cdot\frac{1}{2}h=\frac{1}{4}V,
v=v_{1}+v_{2}=\frac{1}{4}V+\frac{1}{9}V=\frac{13}{36}V.
Следовательно,
\frac{v}{V-v}=\frac{\frac{13}{36}V}{V-\frac{13}{36}V}=\frac{\frac{13}{36}V}{\frac{23}{32}V}=\frac{9}{23}.
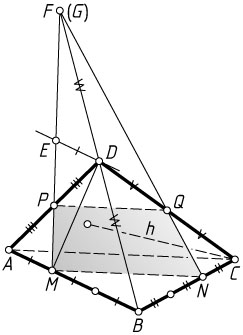
Второй способ. а) Пусть F
— точка пересечения прямых BD
и MP
. Через через вершину D
проведём прямую, параллельную AB
. Пусть она пересекается с отрезком FM
в точке E
. Из равенства треугольников DPE
и APM
получаем, что DE=AM=\frac{1}{2}AB
. Значит, DE
средняя линия треугольника BFM
. Следовательно, BF=2BD
. Аналогично докажем, что если G
— точка пересечения прямых BD
и NQ
, то BG=2BD
. Значит, точки F
и G
совпадают. Следовательно, точки P
, Q
, M
и N
лежат в плоскости пересекающихся прямых MP
и NQ
.
б) Пусть V
, V_{1}
и V_{2}
— объёмы треугольных пирамид DABC
, NFBM
и QFDP
соответственно, S_{\triangle ADB}=S
, а высота треугольной пирамиды DABC
, опущенная из вершины C
, равна h
. Тогда, поскольку NB=\frac{2}{3}CB
(см. задачу 9180), расстояние от точки N
до плоскости ABD
равно \frac{2}{3}h
. Аналогично, расстояние от точки Q
до плоскости ABD
равно \frac{1}{2}h
. Кроме того,
S_{\triangle FBM}=2S_{\triangle BDM}=2\cdot\frac{2}{3}S_{\triangle ABD}=\frac{4}{3}S,
S_{\triangle FDP}=\frac{1}{2}S_{\triangle ADF}=\frac{1}{2}S_{\triangle ABD}=\frac{1}{2}S.
Значит,
V_{1}=\frac{1}{3}S_{\triangle FBM}\cdot\frac{2}{3}h=\frac{1}{3}\cdot\frac{4}{3}S\cdot\frac{2}{3}h=\frac{8}{9}\cdot\frac{1}{3}Sh=\frac{8}{9}V,
V_{2}=\frac{1}{3}S_{\triangle FDP}\cdot\frac{1}{2}h=\frac{1}{3}\cdot\frac{1}{2}S\cdot\frac{1}{2}h=\frac{1}{4}\cdot\frac{1}{3}Sh=\frac{1}{4}V.
Пусть V_{3}
— объём той части пирамиды DABC
, которая содержит точку B
. Тогда
V_{3}=V_{1}-V_{2}=\frac{8}{9}V-\frac{1}{4}V=\frac{23}{36}V,
а объём оставшейся части равен
V-\frac{23}{36}V=\frac{13}{36}V.
Следовательно, искомое отношение равно \frac{13}{23}
.
Примечание. Для доказательства принадлежности указанных четырёх точек одной плоскости можно также воспользоваться задачей 9106.
Источник: ЕГЭ. — 2017, 2 июня
