9603. В правильной пирамиде SABC
точки M
и N
— середины рёбер AB
и BC
соответственно. На боковом ребре SA
отмечена точка K
. Сечение пирамиды плоскостью MNK
является четырёхугольником, диагонали которого пересекаются в точке Q
.
а) Докажите, что точка Q
лежит на высоте пирамиды.
б) Найдите угол между плоскостями MNK
и ABC
, если AB=6
, SA=12
и SK=3
.
Ответ. \arctg2\sqrt{11}
.
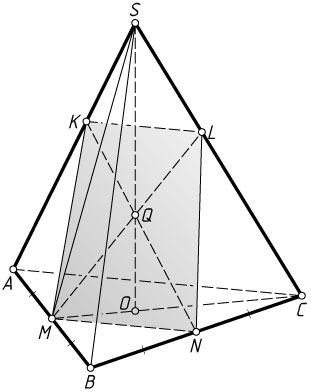
Решение. а) Пусть O
— центр основания пирамиды, L
— точка пересечения плоскости MNK
с прямой SC
.
Прямые SO
и ML
лежат в плоскости CSM
и не параллельны, значит, они пересекаются. Аналогично, прямые SO
и KN
также пересекаются. Кроме того, прямые ML
и KN
пересекаются в точке Q
. Итак, три прямые SO
, ML
и KN
попарно пересекаются и не лежат в одной плоскости. Значит (см. задачу 8018), они проходят через одну точку — точку Q
пересечения диагоналей четырёхугольника MKLN
. Следовательно, точка Q
лежит на высоте SO
пирамиды.
б) Прямая AC
параллельна плоскости MNK
, так как она параллельна прямой MN
, лежащей в этой плоскости (MN
— средняя линия треугольника ABC
). Значит, плоскости ASC
и MNK
пересекаются по прямой KL
, параллельной MN
(см. задачу 8004). Тогда четырёхугольник MKLN
— равнобокая трапеция с основаниями MN
и KL
.
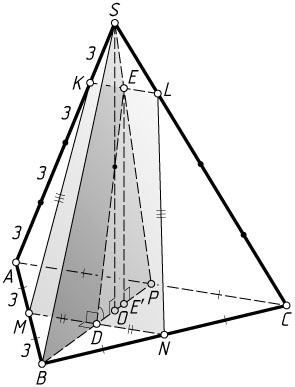
Пусть P
— середина ребра AC
, D
— точка пересечения MN
и BP
, E
— точка пересечения KL
и SP
. Тогда D
— середина BP
, а SE:SP=SK:SA=1:4
. Плоскость BSP
перпендикулярна прямой MN
пересечения плоскостей MNK
и ABC
, поэтому искомый угол — это угол PDE
.
Далее находим:
BP=\frac{AB\sqrt{3}}{2}=3\sqrt{3},~BO=\frac{2}{3}BP=2\sqrt{3},~OP=\frac{1}{3}BP=\sqrt{3},
SO=\sqrt{SB^{2}-BO^{2}}=\sqrt{12^{2}-12}=2\sqrt{33}.
Из параллельности прямых KL
и AC
получаем, что SL=SK=3
. Пусть E'
— ортогональная проекция точки E
на плоскость основания пирамиды. Тогда точка E'
лежит на отрезке OP
, причём
PE':OP=PE:PS=EE':SO=3:4.
Значит,
PE'=\frac{3}{4}OP=\frac{3\sqrt{3}}{4},~EE'=\frac{3}{4}SO=\frac{3\sqrt{33}}{2},
DE'=DP-PE'=\frac{3\sqrt{3}}{2}-\frac{3\sqrt{3}}{4}=\frac{3\sqrt{3}}{4}.
Следовательно,
\tg\angle PDE=\frac{EE'}{DE'}=\frac{\frac{3\sqrt{33}}{2}}{\frac{3\sqrt{3}}{4}}=2\sqrt{11}.
Источник: ЕГЭ. — 2018

