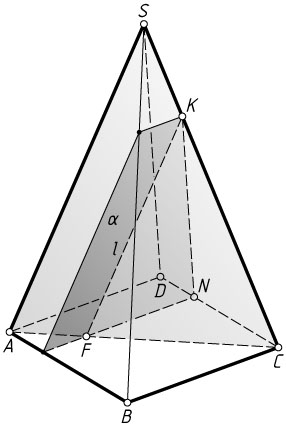
9725. В правильной четырёхугольной пирамиде SABCD
с вершиной S
известно, что AB=7
, AS=14
. На рёбрах CD
и SC
взяты точки N
и K
соответственно, причём DN:NC=SK:KC=2:5
. Плоскость \alpha
содержит прямую NK
и параллельна ребру AS
.
а) Докажите, что плоскость \alpha
параллельна BC
.
б) Найдите расстояние от точки B
до плоскости \alpha
.
Ответ. \frac{\sqrt{210}}{3}
.
Решение. а) Плоскость ASC
проходит через прямую AS
, параллельную плоскости \alpha
, и имеет с плоскостью \alpha
общую точку K
, значит, плоскости ASC
и \alpha
пересекаются по прямой l
, параллельной AS
(см. задачу 8003).
Пусть прямые l
и AC
пересекаются в точке F
. Тогда по теореме о пропорциональных отрезках AF:FC=SK:KC=2:5
, а так как DN:NC=2:5=AF:FC
, то FN\parallel AD\parallel BC
. Следовательно, прямая BC
параллельна плоскости \alpha
по признаку параллельности прямой и плоскости (см. задачу 8002).
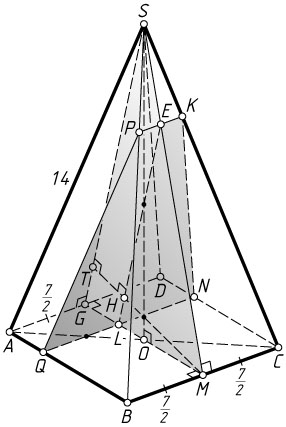
б) Пусть O
— центр квадрата ABCD
, Q
— точка пересечения NF
и AB
, M
и G
— середины BC
и AD
соответственно, P
— точка пересечения плоскости \alpha
с ребром SB
, KP\parallel NQ\parallel BC
, E
и L
— середины PK
и NQ
соответственно. Тогда
SO=\sqrt{SA^{2}-OA^{2}}=\sqrt{14^{2}-\left(\frac{7\sqrt{2}}{2}\right)^{2}}=7\sqrt{4-\frac{1}{2}}=\frac{7\sqrt{7}}{\sqrt{2}},
SG=\sqrt{SA^{2}-AG^{2}}=\sqrt{14^{2}-\left(\frac{7}{2}\right)^{2}}=7\sqrt{4-\frac{1}{4}}=\frac{7\sqrt{15}}{2}.
Точка B
лежит на прямой BC
, параллельной плоскости \alpha
, значит, расстояние от точки B
до этой плоскости равно расстоянию от любой точки прямой BC
до плоскости \alpha
, например, от середины M
ребра BC
.
Пусть MT
— высота равнобедренного треугольника MSG
. Поскольку SE:EM=SK:KC=2:5
и GL:LM=DN:NC=2:5
, прямые EL
и SG
параллельны, поэтому MT\perp EL
, а так как прямая MT
лежит в плоскости MSG
, перпендикулярной прямой QN
, то MT\perp QN
. Следовательно, прямая MT
перпендикулярна плоскости \alpha
. Пусть H
— точка пересечения MT
и EL
. Тогда MH\perp\alpha
, а расстояние от точки M
до плоскости \alpha
равно длине отрезка MH
.
Из равнобедренного треугольника MSG
получаем, что GM\cdot SO=SG\cdot MT
(удвоенная площадь треугольника MSG
), откуда
MT=\frac{GM\cdot SO}{SG}=\frac{7\cdot\frac{7\sqrt{7}}{\sqrt{2}}}{\frac{7\sqrt{15}}{2}}=\frac{7\sqrt{14}}{\sqrt{15}},
а так как треугольник MEL
подобен треугольнику MSG
с коэффициентом \frac{ML}{MG}=\frac{5}{7}
, то
MH=\frac{5}{7}\cdot\frac{7\sqrt{14}}{\sqrt{15}}=\frac{\sqrt{14}\sqrt{5}}{\sqrt{3}}=\frac{\sqrt{210}}{3}.
Источник: ЕГЭ. — 2019, 29 мая, задача 14

